题目内容
7.已知n∈N+,函数f(n)=$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n+1}$,则f(2)-f(1)=-$\frac{1}{20}$;f(n+1)-f(n)=-$\frac{1}{4{n}^{2}+10n+6}$.分析 由已知条件分别代入1,2,n,n+1,然后进行化简求值即可.
解答 解:∵函数f(n)=$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n+1}$,
∴f(2)-f(1)=$\frac{1}{3}+\frac{1}{4}+\frac{1}{5}-\frac{1}{2}-\frac{1}{3}$=-$\frac{1}{20}$.
f(n+1)-f(n)=$\frac{1}{n+2}+…+\frac{1}{2n+1}$+$\frac{1}{2n+2}+\frac{1}{2n+3}$-($\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n+1}$)=$-\frac{1}{{4{n^2}+10n+6}}$.
故答案为:$-\frac{1}{20}$;$-\frac{1}{{4{n^2}+10n+6}}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
15.已知集合$A=\left\{{x|sin\frac{{{π_{\;}}x}}{3}<\frac{1}{2}}\right\}$,B={x|(x+1)(x-2)<0},则(∁RA)∩B=( )
| A. | $(-1,\frac{1}{2})$ | B. | [$\frac{1}{2}$,$\frac{5}{2}$] | C. | $[{\frac{1}{2},2})$ | D. | (-1,2) |
15.直线y=2x+3与双曲线x2-y2=1交于A、B两点,则相交弦的弦长为( )
| A. | $\frac{\sqrt{19}}{3}$ | B. | $\frac{2\sqrt{10}}{3}$ | C. | $\frac{\sqrt{30}}{3}$ | D. | $\frac{2\sqrt{30}}{3}$ |
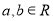 ,则“
,则“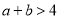 ”是“
”是“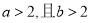 ”的( )
”的( )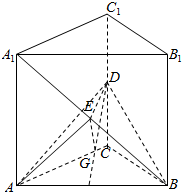 如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.