题目内容
6.某年青教师近五年内所带班级的数学平均成绩统计数据如表:| 年份x年 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
(2)利用(1)中所求出的直线方程预测该教师2015年所带班级的数学平均成绩.
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
分析 (1)先利用数据平均值的公式求出x,y的平均值,再计算b,a的值,即可求出平均分与年份之间的回归直线方程$\hat y=bx+a$,根据b>0,可得成绩与年份成正相关关系;
(2)x=2015,代入回归直线方程,即可预测该教师2015年所带班级的数学平均成绩.
解答 解:(1)由题意,$\overline{x}$=$\frac{1}{5}$(2009+2010+2011+2012+2013)=2011,$\overline{y}$=$\frac{1}{5}$(97+98+103+108+109)=103,…(2分)
b=$\frac{(-2)(-6)+(-1)(-5)+0×0+1×5+2×6}{(-2)^{2}+{1}^{2}+{0}^{2}+{1}^{2}+{2}^{2}}$=3.4…(4分)
a=103-3.4×2011=-6734.4…(6分)
∴y=3.4x-6734.4,
∵b>0
∴成绩与年份成正相关关系…(8分)
(2)y=3.4x-6734.4=3.4×2.15-6734.4=116.6
∴预测2015年该班的数学平均成绩为116.(6分) …(12分)
点评 解决线性回归直线的方程,利用最小二乘法求出直线的截距和斜率,利用回归直线方程可预测.

练习册系列答案
相关题目
15.直线y=2x+3与双曲线x2-y2=1交于A、B两点,则相交弦的弦长为( )
| A. | $\frac{\sqrt{19}}{3}$ | B. | $\frac{2\sqrt{10}}{3}$ | C. | $\frac{\sqrt{30}}{3}$ | D. | $\frac{2\sqrt{30}}{3}$ |
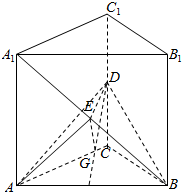 如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.