题目内容
10.已知${a^{\frac{2}{3}}}=\frac{4}{9}$,其中a>0,则$lo{g_a}\frac{4}{9}$=$\frac{2}{3}$; $lo{g_a}\frac{2}{3}$=$\frac{1}{3}$.分析 根据指数式与对数式的互化就去即可.
解答 解:∵a${\;}^{\frac{2}{3}}$=$\frac{4}{9}$,
∴log${\;}_{a}\frac{4}{9}$=$\frac{2}{3}$'
∴log${\;}_{a}\frac{4}{9}$=log${\;}_{a}(\frac{2}{3})^{2}$=2loga$\frac{2}{3}$,
∴log${\;}_{a}\frac{2}{3}$=$\frac{1}{3}$.
故答案为:$\frac{2}{3},\frac{1}{3}$.
点评 本题主要考查指数式与对数式的互化,属于基础题.

练习册系列答案
相关题目
18.已知等比数列{an}中,若a4=10,a8=$\frac{5}{2}$,那么a6=( )
| A. | -5 | B. | 5 | C. | ±5 | D. | 25 |
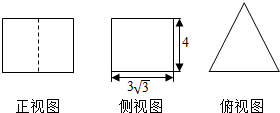 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的表面积为$72+18\sqrt{3}$.则这个棱柱体积为36$\sqrt{3}$.
若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的表面积为$72+18\sqrt{3}$.则这个棱柱体积为36$\sqrt{3}$.