题目内容

已知△ABC为等边三角形，AB=2，设点P，Q满足
AP
=λ
AB
，
AQ
=（1-λ）
AC
，λ∈R，若
BQ
•
CP
=-
3
2
，则λ=
 
．
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：由已知条件用向量
AB
，
AC
表示向量
BQ
，
CP
，代入
BQ
•
CP
=-
3
2
，由平面向量的数量积能求出λ的值．
解答： 解：∵点P，Q满足
AP
=λ
AB
，
AQ
=（1-λ）
AC
，λ∈R，
∴
BQ
=
AQ
-
AB
=(1-λ)
AC
-
AB
，
CP
=
AP
-
AC
=λ
AB
-
AC
，
又∵△ABC为等边三角形，AB=2，
BQ
•
CP
=-
3
2
，
∴|
AB
|=|
AC
|=2，＜
AB
，
AC
＞=60°，
∴
AB
•
AC
=|
AB
|•|
AC
|•cos60°=2×2×
1
2
=2，
∴[(1-λ)
AC
-
AB
](λ
AB
-
AC
)=-
3
2
，
∴λ|
AB
|2 +(λ2-λ-1)
AB
•
AC
+(1-λ)|
AC
|2=
3
2
，
∴4λ+2（λ2-λ-1）+4（1-λ）=
3
2
，
解得λ=
1
2
．
故答案为：
1
2
．
点评：本题考查平面向量的数量积的运算，是中档题，解题时要认真审题，注意数形结合思想的合理运用．
练习册系列答案
相关题目
已知函数f（x）=x2+ax+3，g（x）=（6+a）•2x-1
（Ⅰ）若f（1）=f（3），求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，判断函数F（x）=
2
1+g(x)
的单调性，并给出证明；
（Ⅲ）当x∈[-2，2]时，f（x）≥a（a∉（-4，4））恒成立，求实数a的最小值．
（坐标系与参数方程选做题）已知P是曲线M：
x=1+2cosθ
y=2+2sinθ
（θ为参数）上的点，Q是曲线L：
x=4t+5
y=3t+1
（t为参数）上的点，则|PQ|的最小值为
 
．
比较大小：2-11
 
2-12．
y=2exsinx，则y′=
 
．
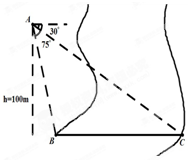如图，在气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，若此时的气球高度是100m，则河流在B，C两地的宽度为
 
．
方程
x2
k-3
+
y2
5-k
=1表示焦点在x轴上的椭圆，则k的取值范围是
 
．
若实数x，y满足2x+3y=2，则4x+8y的最小值为
 
．
cos210°等于（　　）
A、
1
2
B、-
1
2
C、-
3
2
D、
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网