某地铁站每隔10分钟有一趟地铁通过.乘客到达地铁站的任一时刻是等可能的.乘客候车不超过2分钟的概率( )A．$\frac{1}{10}$B．$\frac{1}{6}$C．$\frac{1}{5}$D．$\frac{1}{4}$ 题目和参考答案——青夏教育精英家教网—

题目内容

8．某地铁站每隔10分钟有一趟地铁通过，乘客到达地铁站的任一时刻是等可能的，乘客候车不超过2分钟的概率（　　）

A．

$\frac{1}{10}$

B．

$\frac{1}{6}$

C．

$\frac{1}{5}$

D．

$\frac{1}{4}$

分析根据题意确定出基本事件对应的“几何度量”N（A）为2，再求出总的基本事件对应的“几何度量”N为10，利用几何概型的概率公式，求出所求概率即可．

解答解：由题意可得：乘客到达汽车站候车时间最多为10min，
又因为乘客候车时间不超过2min，
∴乘客候车时间不超过2min的概率是P=$\frac{2}{10}$=$\frac{1}{5}$．
故选C．

点评此题考查了几何概型，解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=$\frac{N（A）}{N}$求解，考查计算能力，属于基础题．

练习册系列答案

19．某工厂要建造一个长方体无盖贮水池，其容积为6400m³，深为4m，如果池底每1m²的造价为300元，池壁每1m²的造价为240元，问怎样设计水池能使总造价最低，最低总造价是多少元？

16．设点P是椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$上的一点，M、N分别是两圆：（x+3）²+y²=1和（x-3）²+y²=1上的点，则|PM|+|PN|的最大值为（　　）

3．一条线段AB的长等于2a，两端点A、B分别在x轴、y轴上滑动，点M在线段AB上，且|AM|﹕|MB|=1﹕2，则点M的轨迹方程为$\frac{9}{4}$x²+9y²=4a²．

4．

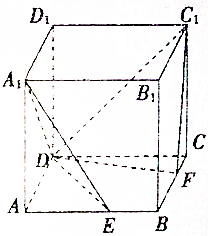如图所示，ABCD-A₁B₁C₁D₁是棱长为6的正方体，E，F分别是棱AB，BC上的动点，且AE=BF．当A₁，E，F，C₁共面时，平面A₁DE与平面C₁DF所成锐二面角的余弦值为（　　）

$\frac{2\sqrt{6}}{5}$

11．已知奇函数f（x）的定义域为（-∞，0）∪（0，+∞），且不等式$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0对任意两个不相等的正实数x₁，x₂都成立，在下列不等式中，正确的是（　　）

8．在（2x+a）⁵的展开式中，含x²项的系数等于320，则$\int_0^a{（{e^x}+2x）dx}$等于（　　）

9．化简：
（1）sin（$\frac{π}{6}$-2π）cos（$\frac{π}{4}$+π）
（2）sin（$\frac{π}{4}$+$\frac{5π}{2}$）

试题分类