题目内容
(1)设直线l1:y=2x与直线l2:x+y=3交于点P,当直线l过P点,且原点O到直线l的距离为1时,求直线l的方程.
(2)已知圆C:x2+y2+4x-8y+19=0,过点P(-4,5)作圆C的切线,求切线方程.
(2)已知圆C:x2+y2+4x-8y+19=0,过点P(-4,5)作圆C的切线,求切线方程.
考点:圆的切线方程,直线的一般式方程
专题:综合题,直线与圆
分析:(1)考虑两种情况:①斜率不存在即所求直线与y轴平行时,容易直线的方程;②斜率存在时,设出直线的斜截式,然后利用点到直线的距离公式列出原点到直线l的距离的方程,求出斜率k即可得到方程;
(2)化圆的方程为标准方程,利用点线距离等于半径,可求切线方程,应注意有两条.
(2)化圆的方程为标准方程,利用点线距离等于半径,可求切线方程,应注意有两条.
解答:
解:(1)当过点A(1,2)的直线与x轴垂直时,
则点A(1,2)到原点的距离为1,所以x=1为所求直线方程.
当过点A(1,2)且与x轴不垂直时,可设所求直线方程为y-2=k(x-1),
即:kx-y-k+2=0,由题意有
=1,解得k=
,
故所求的直线方程为y-2=
(x-1),即3x-4y+5=0.
综上,所求直线方程为x=1或3x-4y+5=0.
(2)由C:x2+y2+4x-8y+19=0得圆的标准方程为(x+2)2+(y-4)2=1.
①显然y=5为圆的切线
②另一方面,设过(-4,5)的圆的切线方程为y-5=k(x+4),即kx-y+5+4k=0;
所以d=
=1,解得k=-
,∴切线方程为4x+3y+1=0.
综上所述,切线方程为y=5或4x+3y+1=0.
则点A(1,2)到原点的距离为1,所以x=1为所求直线方程.
当过点A(1,2)且与x轴不垂直时,可设所求直线方程为y-2=k(x-1),
即:kx-y-k+2=0,由题意有
| |-k+2| | ||
|
| 3 |
| 4 |
故所求的直线方程为y-2=
| 3 |
| 4 |
综上,所求直线方程为x=1或3x-4y+5=0.
(2)由C:x2+y2+4x-8y+19=0得圆的标准方程为(x+2)2+(y-4)2=1.
①显然y=5为圆的切线
②另一方面,设过(-4,5)的圆的切线方程为y-5=k(x+4),即kx-y+5+4k=0;
所以d=
| |-2k-4+5+4k| | ||
|
| 4 |
| 3 |
综上所述,切线方程为y=5或4x+3y+1=0.
点评:本题考查圆的切线方程的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,则z=3x-y的最大值为( )
|
| A、11 | B、7 | C、3 | D、-5 |
若幂函数y=xα在 (0,+∞)上是增函数,则α一定( )
| A、α>0 | B、α<0 |
| C、α>1 | D、不确定 |
已知a,b,c∈R,那么下列命题中一定正确的是( )
A、若
| ||||
| B、若a>b,c>d,则a-c>b-d | ||||
| C、若a>-b,则c-a<c+b | ||||
| D、若a>b,则a2>b2 |
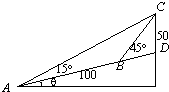 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测测建筑物顶端C对于山坡的斜度为45°,建筑物的高CD为50米,求此山对于地面的倾斜角θ的余弦值(结果保留最简根式).
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测测建筑物顶端C对于山坡的斜度为45°,建筑物的高CD为50米,求此山对于地面的倾斜角θ的余弦值(结果保留最简根式).