题目内容
已知0≤θ≤
,当点(1,cosθ)到直线l:xsinθ+ycosθ-1=0的距离是
时,直线l的斜率为 .
| π |
| 2 |
| 1 |
| 4 |
考点:点到直线的距离公式
专题:直线与圆
分析:由点到直线的距离公式得
=|sinθ-sin2θ|=
,由此得到sinθ=
,cosθ=
,从而能求出直线l的斜率.
| |sinθ+cos2θ-1| | ||
|
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
解答:
解:∵0≤θ≤
,当点(1,cosθ)到直线l:xsinθ+ycosθ-1=0的距离是
,
∴
=|sinθ-sin2θ|=
,
解得sinθ=
,∴cosθ=
=
,
∴直线l的斜率k=-
=-
=
.
故答案为:
.
| π |
| 2 |
| 1 |
| 4 |
∴
| |sinθ+cos2θ-1| | ||
|
| 1 |
| 4 |
解得sinθ=
| 1 |
| 2 |
1-
|
| ||
| 2 |
∴直线l的斜率k=-
| sinθ |
| cosθ |
| ||||
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查直线的斜率的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
正三棱柱有一个半径为
cm的内切球,则此棱柱的体积是( )
| 3 |
A、9
| ||
| B、54cm3 | ||
| C、27cm3 | ||
D、18
|
圆心在点C(2,0),半径 R=
的圆的标准方程是( )
| 10 |
A、(x-2)2+y2=
| ||
B、x2+(y-2)2=
| ||
| C、x2+(y-2)2=10 | ||
| D、(x-2)2+y2=10 |
经过直线2x-y=0与直线x+y-6=0的交点,且与直线2x+y-1=0平行的直线方程是( )
| A、x-2y+6=0 |
| B、x-2y-6=0 |
| C、2x+y-8=0 |
| D、x+2y+8=0 |
函数f(x)=x4+2x的导数f′(x)=( )
| A、x3+2 |
| B、4x3 |
| C、4x3+2 |
| D、4x3+2x |

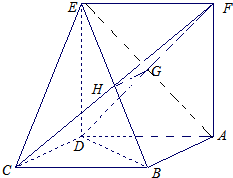 平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.