题目内容
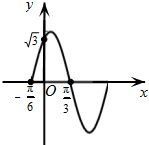 如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤
如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤| π |
| 2 |
| 3 |
(Ⅰ)求函数的解析式;
(Ⅱ)若f(
| θ |
| 2 |
| π |
| 6 |
| cos(π+θ) |
| [cos(π-θ)-1]•cosθ |
sin(-
| ||
| cosθ•cos(π-θ)+cos(θ-2π) |
考点:正弦函数的图象,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)根据图象确定A,ω 和φ的值即可求函数的解析式;
(Ⅱ)利用三角函数的诱导公式进行化简即可.
(Ⅱ)利用三角函数的诱导公式进行化简即可.
解答:
解:( I)∵0≤φ≤
,
∴由五点对应法得
,解得ω=2,φ=
,
则f(x)=Asin(ωx+φ)=Asin(2x+
),
∵图象与y轴交于点(0,
),
∴f(0)=Asin
=
,解得A=2,
故f(x)=2sin(2x+
).
( II)∵f(
-
)=1,
∴得sinθ=
,
则
-
=
-
=
-
=-
=-8.
| π |
| 2 |
∴由五点对应法得
|
| π |
| 3 |
则f(x)=Asin(ωx+φ)=Asin(2x+
| π |
| 3 |
∵图象与y轴交于点(0,
| 3 |
∴f(0)=Asin
| π |
| 3 |
| 3 |
故f(x)=2sin(2x+
| π |
| 3 |
( II)∵f(
| θ |
| 2 |
| π |
| 6 |
∴得sinθ=
| 1 |
| 2 |
则
| cos(π+θ) |
| [cos(π-θ)-1]•cosθ |
sin(-
| ||
| cosθ•cos(π-θ)+cos(θ-2π) |
| -cosθ |
| cosθ(-1-cosθ) |
| -cosθ |
| -cosθ•cosθ+cosθ |
| 1 |
| 1+cosθ |
| 1 |
| cosθ-1 |
| 2 |
| sin2θ |
点评:本题主要考查三角函数解析式的求解以及诱导公式的应用,根据图象确定A,ω 和φ的值是解决本题的关键.

练习册系列答案
相关题目
12件同类产品中,有10件是正品,2件是次品,从中任意抽出3件,与“抽得1件次品2件正品”互斥而不对立的事件是( )
| A、抽得3件正品 |
| B、抽得至少有1件正品 |
| C、抽得至少有1件次品 |
| D、抽得3件正品或2件次品1件正品 |
正三棱柱有一个半径为
cm的内切球,则此棱柱的体积是( )
| 3 |
A、9
| ||
| B、54cm3 | ||
| C、27cm3 | ||
D、18
|
经过直线2x-y=0与直线x+y-6=0的交点,且与直线2x+y-1=0平行的直线方程是( )
| A、x-2y+6=0 |
| B、x-2y-6=0 |
| C、2x+y-8=0 |
| D、x+2y+8=0 |
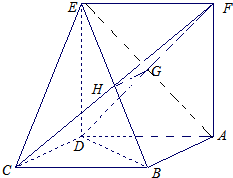 平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.