题目内容
定义函数d(x)=
,f(x)=1gx,那么下列命题中正确的序号是 .(把所有可能的图的序号都填上).
①函数d(x)为偶函数;②函数d(x)为周期函数,且任何非零实数均为其周期;
③方程d(x)=f(x)有两个不同的根.
|
①函数d(x)为偶函数;②函数d(x)为周期函数,且任何非零实数均为其周期;
③方程d(x)=f(x)有两个不同的根.
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:由已知中函数d(x)=
,f(x)=1gx,分析d(x)的奇偶性与周期性,可判断①②;分析方程d(x)=f(x)根的个数,可判断③.
|
解答:
解:∵函数d(x)=
,f(x)=1gx,
对于①,当x∈Q时,d(-x)=d(x)=1,
当x∉Q时,d(-x)=d(x)=0,
即d(-x)=d(x)恒成立,
函数d(x)为偶函数,故正确;
对于②,函数d(x)为周期函数,且任何非零有理数均为其周期,故错误;
对于③,当且仅当x=10时,d(x)=f(x),故方程d(x)=f(x)仅有一个根,故错误.
故答案为:①
|
对于①,当x∈Q时,d(-x)=d(x)=1,
当x∉Q时,d(-x)=d(x)=0,
即d(-x)=d(x)恒成立,
函数d(x)为偶函数,故正确;
对于②,函数d(x)为周期函数,且任何非零有理数均为其周期,故错误;
对于③,当且仅当x=10时,d(x)=f(x),故方程d(x)=f(x)仅有一个根,故错误.
故答案为:①
点评:本题以命题的真假判断为载体考查了函数的奇偶性,周期性,函数零点与方程根的关系,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
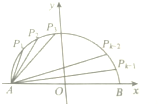 如图,AB是圆x2+y2=16的直径,把线段AB分成k(k≥4,k∈Z)等份,过每个分点作x轴的垂线交圆的上半部分于P1,P2,…,Pk-1,共k-1个点,令an=|APn|,n=1,2,3,…,k-1.则( )
如图,AB是圆x2+y2=16的直径,把线段AB分成k(k≥4,k∈Z)等份,过每个分点作x轴的垂线交圆的上半部分于P1,P2,…,Pk-1,共k-1个点,令an=|APn|,n=1,2,3,…,k-1.则( )| A、{an}是等差数列 |
| B、{an}是等比数列 |
| C、当k=8时,a12+a22+a32+…+a72=224 |
| D、当k=8时,a1+a2+a3+…+a7=224 |
若α=390°,则角α的终边落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |