题目内容
设二次函数f(x)=ax2+(2b+1)x-a-2(a,b∈R,a≠0)在[3,4]上至少有一个零点,则a2+b2的最小值为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:把等式看成关于a,b的直线方程:(x2-1)a+2xb+x-2=0,根据直线上一点(a,b)到原点的距离大于等于原点到直线的距离,得一不等式,对式子进行恰当变形后,利用函数的单调性可求得a2+b2的最小值.
解答:
解:把等式看成关于a,b的直线方程:(x2-1)a+2xb+x-2=0,
由于直线上一点(a,b)到原点的距离大于等于原点到直线的距离,
即
≥
,
∴a2+b2≥
=
≥
,
因为x-2+
在x∈[3,4]是减函数,上述式子在x=3,a=-
,b=-
时取等号,
故a2+b2的最小值为
.
故答案为:
由于直线上一点(a,b)到原点的距离大于等于原点到直线的距离,
即
| a2+b2 |
| |x-2| | ||
|
∴a2+b2≥
| (x-2)2 |
| (x2-1)2+(2x)2 |
| 1 | ||
(x-2+
|
| 1 |
| 100 |
因为x-2+
| 5 |
| x-2 |
| 2 |
| 25 |
| 3 |
| 50 |
故a2+b2的最小值为
| 1 |
| 100 |
故答案为:
| 1 |
| 100 |
点评:本题考查二次函数的性质、函数的单调性及不等式知识,考查学生灵活运用知识解决问题的能力,能力要求较高.

练习册系列答案
相关题目

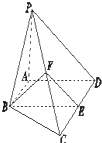 (文科)如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥AD,AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点.求证:
(文科)如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥AD,AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点.求证: