题目内容
设f(x)=
+blnx.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线方程为y=x+1,求a,b的值;
(Ⅱ)当a=e,b=1时,求f(x)的单调区间与极值.
| a |
| ex |
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线方程为y=x+1,求a,b的值;
(Ⅱ)当a=e,b=1时,求f(x)的单调区间与极值.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)对f(x)求导,根据f(x)在点(1,f(1))处的切线方程,求出a、b的值;
(Ⅱ)a=e,b=1时,求出f(x)的导数,利用导数来判定f(x)的单调区间,利用单调性求出f(x)的极小值.
(Ⅱ)a=e,b=1时,求出f(x)的导数,利用导数来判定f(x)的单调区间,利用单调性求出f(x)的极小值.
解答:
解:(Ⅰ)对f(x)求导,得f′(x)=
-
;
由f′(1)=b-
=1,f(1)=
=1+1=2,
解得a=2e,b=3;
(Ⅱ)∵函数f(x)的定义域是(0,+∞),
当a=e,b=1时,f(x)=
+lnx,f′(x)=
-
=
;
令g(x)=ex-ex,求导得g'(x)=ex-e;
当x∈(0,1)时,g'(x)<0,则f'(x)<0,f(x)是减函数;
当x∈(1,+∞)时,g'(x)>0,则f'(x)>0,f(x)是增函数;
∴f(x)的单调增区间是(1,+∞),减区间是(0,1);
∴当x=1时,f(x)有极小值f(1)=1.
| b |
| x |
| a |
| ex |
由f′(1)=b-
| a |
| e |
| a |
| e |
解得a=2e,b=3;
(Ⅱ)∵函数f(x)的定义域是(0,+∞),
当a=e,b=1时,f(x)=
| e |
| ex |
| 1 |
| x |
| e |
| ex |
| ex-ex |
| xex |
令g(x)=ex-ex,求导得g'(x)=ex-e;
当x∈(0,1)时,g'(x)<0,则f'(x)<0,f(x)是减函数;
当x∈(1,+∞)时,g'(x)>0,则f'(x)>0,f(x)是增函数;
∴f(x)的单调增区间是(1,+∞),减区间是(0,1);
∴当x=1时,f(x)有极小值f(1)=1.
点评:本题考查了导数的综合应用问题,解题时应利用导数来研究函数的单调性,并且利用函数的单调性来求函数的极值,是综合性题目.

练习册系列答案
相关题目
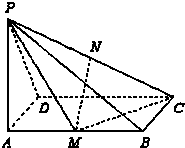 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1 正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依次得到一系列的正方形,如右图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,爬行了10条线段.则这10条线段的长度的平方和是
正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依次得到一系列的正方形,如右图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,爬行了10条线段.则这10条线段的长度的平方和是