题目内容
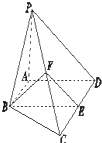 (文科)如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥AD,AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点.求证:
(文科)如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥AD,AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点.求证:(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
考点:平面与平面垂直的判定,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)根据条件,利用平面和平面垂直的性质定理可得PA⊥平面ABCD;
(2)根据已知条件判断ABED为平行四边形,故有BE∥AD,再利用直线和平面平行的判定定理证得BE∥平面PAD.
(3)先证明ABED为矩形,可得BE⊥CD.现证CD⊥平面PAD,可得CD⊥PD,再由三角形中位线的性质可得EF∥PD,从而证得CD⊥EF.利用直线和平面垂直的判定定理证得CD⊥平面BEF,再由平面和平面垂直的判定定理证得平面BEF⊥平面PCD.
(2)根据已知条件判断ABED为平行四边形,故有BE∥AD,再利用直线和平面平行的判定定理证得BE∥平面PAD.
(3)先证明ABED为矩形,可得BE⊥CD.现证CD⊥平面PAD,可得CD⊥PD,再由三角形中位线的性质可得EF∥PD,从而证得CD⊥EF.利用直线和平面垂直的判定定理证得CD⊥平面BEF,再由平面和平面垂直的判定定理证得平面BEF⊥平面PCD.
解答:
证明:(1)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
且PA⊥AD,PA?平面PAD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE,
所以ABED为平行四边形,
所以BE∥AD.
又因为BE?平面PAD,AD?平面PAD,
所以BE∥平面PAD.
(3)因为AB⊥AD,而且ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,
所以PA⊥CD.
又因为AD∩PA=A,所以CD⊥平面PAD,
所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF,
所以CD⊥EF,
所以CD⊥平面BEF,
所以平面BEF⊥平面PCD.
且PA⊥AD,PA?平面PAD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE,
所以ABED为平行四边形,
所以BE∥AD.
又因为BE?平面PAD,AD?平面PAD,
所以BE∥平面PAD.
(3)因为AB⊥AD,而且ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,
所以PA⊥CD.
又因为AD∩PA=A,所以CD⊥平面PAD,
所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF,
所以CD⊥EF,
所以CD⊥平面BEF,
所以平面BEF⊥平面PCD.
点评:本题主要考查直线和平面垂直的判定定理,直线和平面平行的判定定理,平面和平面垂直的判定定理、性质定理的应用,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.
已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.