题目内容
已知函数f(x)的定义域是(0,+∞),且当x>0时,满足
>f′(x).
(Ⅰ)判断函数y=
在(0,+∞)上的单调性,并说明理由;
(Ⅱ)三个同学对问题“已知m、n∈N*且n>m≥2,证明(1+m)n>(1+n)m”提出各自的解题思路.
甲说:“用二项式定理将不等式的左右两边展开,运用放缩法即可证明”
乙说:“通过转化,构造函数,利用函数的单调性即可证明”
参考上述解题思路,结合自己的知识,请你证明此不等式.
| f(x) |
| x |
(Ⅰ)判断函数y=
| f(x) |
| x |
(Ⅱ)三个同学对问题“已知m、n∈N*且n>m≥2,证明(1+m)n>(1+n)m”提出各自的解题思路.
甲说:“用二项式定理将不等式的左右两边展开,运用放缩法即可证明”
乙说:“通过转化,构造函数,利用函数的单调性即可证明”
参考上述解题思路,结合自己的知识,请你证明此不等式.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)中通过求导函数,判断出其导数值为负,从而得出是单调减函数;(2)通过转化,构造函数,利用函数的单调性即可证明.
解答:
解:(1)∵y′=[
]′=
,
又∵
>f′(x),
所以当x>0时,f(x)>xf′(x)
∴
<0即:y′<0,
因此函数y=
在(0,+∞)上是单调递减函数.
(2)∵n>m≥2,
设f(x)=
(x∈R,且x≥2),
∴f(x)=
,
∵x≥2,
∴0<
<1,
∴ln(1+x)≥ln(1+2)=ln3>1,
∴f′(x)<0,
∴f(x)在[2,+∞)上是减函数
∵n>m≥2,
∴
>
∴nln(1+m)>mln(1+n),
∴(1+m)n>(1+n)m.
| f(x) |
| x |
| xf′(x)-f(x) |
| x2 |
又∵
| f(x) |
| x |
所以当x>0时,f(x)>xf′(x)
∴
| xf′(x)-f(x) |
| x2 |
因此函数y=
| f(x) |
| x |
(2)∵n>m≥2,
设f(x)=
| ln(1+x) |
| x |
∴f(x)=
| ||
| x2 |
∵x≥2,
∴0<
| x |
| 1+x |
∴ln(1+x)≥ln(1+2)=ln3>1,
∴f′(x)<0,
∴f(x)在[2,+∞)上是减函数
∵n>m≥2,
∴
| ln(1+m) |
| m |
| ln(1+n) |
| n |
∴nln(1+m)>mln(1+n),
∴(1+m)n>(1+n)m.
点评:本题考察了函数的单调性,导数的应用,不等式的证明,是一道综合题.

练习册系列答案
相关题目
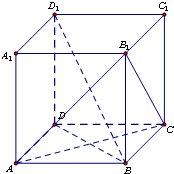 已知正方体ABCD-A1B1C1D1中,求证:
已知正方体ABCD-A1B1C1D1中,求证: 已知函数f(x)=Acos(ωx+φ)的图象如图所示(A>0,ω>0,|φ|<
已知函数f(x)=Acos(ωx+φ)的图象如图所示(A>0,ω>0,|φ|<