题目内容
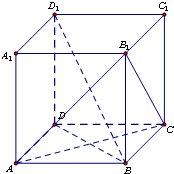 已知正方体ABCD-A1B1C1D1中,求证:
已知正方体ABCD-A1B1C1D1中,求证:(1)AC⊥平面B1D1DB;
(2)BD1⊥平面ACB1.
考点:直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)由AC⊥BD,AC⊥BB1,由此能够证明AC⊥平面B1D1DB.
(2)利用线面垂直的判定与性质,证明AC⊥BD1,AB1⊥BD1,即可证得结论.
(2)利用线面垂直的判定与性质,证明AC⊥BD1,AB1⊥BD1,即可证得结论.
解答:
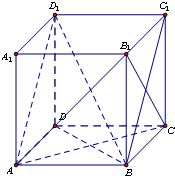 证明:(1)正方体ABCD-A1B1C1D1中,B1B⊥平面ABCD,AC?平面ABCD,
证明:(1)正方体ABCD-A1B1C1D1中,B1B⊥平面ABCD,AC?平面ABCD,
∴AC⊥BB1,
又∵AC⊥BD,BD∩B1B=B,
∴AC⊥平面B1D1DB;
(2)∵AC⊥平面BDD1B1,
又BD1?平面BDD1B1,
∴AC⊥BD1,同理可证AB1⊥BD1,
∵AC与AB1是平面ACB1内的两条相交直线,
∴BD1⊥平面ACB1.
 证明:(1)正方体ABCD-A1B1C1D1中,B1B⊥平面ABCD,AC?平面ABCD,
证明:(1)正方体ABCD-A1B1C1D1中,B1B⊥平面ABCD,AC?平面ABCD,∴AC⊥BB1,
又∵AC⊥BD,BD∩B1B=B,
∴AC⊥平面B1D1DB;
(2)∵AC⊥平面BDD1B1,
又BD1?平面BDD1B1,
∴AC⊥BD1,同理可证AB1⊥BD1,
∵AC与AB1是平面ACB1内的两条相交直线,
∴BD1⊥平面ACB1.
点评:本题考查线面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
观察下列各式:已知a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则归纳猜测a7+b7=( )
| A、26 | B、27 | C、28 | D、29 |