题目内容
设函数f（x）=x[
+
]（a＞1）．
（Ⅰ）求函数的定义域A；
（Ⅱ）判断函数的奇偶性，并给予证明；
（Ⅲ）如果对于定义域A中的任意的x，f（x）＞m恒成立，求实数m的取值范围．
| 1 |
| a |
| 2 |
| a(ax-1) |
（Ⅰ）求函数的定义域A；
（Ⅱ）判断函数的奇偶性，并给予证明；
（Ⅲ）如果对于定义域A中的任意的x，f（x）＞m恒成立，求实数m的取值范围．
考点：函数奇偶性的性质,函数的定义域及其求法,函数奇偶性的判断
专题：综合题,函数的性质及应用
分析：（Ⅰ）由ax-1≠0可求函数定义域；
（Ⅱ）由奇偶性的定义可作出判断；
（Ⅲ）对于定义域A中的任意的x，f（x）＞m恒成立，等价于f（x）min≥m，当x＞0时，由指数函数的性质可判断f（x）＞0，由偶函数性质可知x＜0时也有f（x）＞0从而可得f（x）min=0．
（Ⅱ）由奇偶性的定义可作出判断；
（Ⅲ）对于定义域A中的任意的x，f（x）＞m恒成立，等价于f（x）min≥m，当x＞0时，由指数函数的性质可判断f（x）＞0，由偶函数性质可知x＜0时也有f（x）＞0从而可得f（x）min=0．
解答：
解：（Ⅰ）由ax-1≠0，得x≠0，
∴函数f（x）的定义域为（-∞，0）∪（0，+∞），即A=（-∞，0）∪（0，+∞）；
（Ⅱ）由（Ⅰ）知f（x）的定义域关于原点对称，
又f（-x）=-x[
+
]=x[-
+
]=x[-
+
]=x[-
+
]=x[
+
]=f（x），
∴f（x）为偶函数；
（Ⅲ）当x＞0时，∵a＞1，∴ax-1＞0，
∴
+
＞0，x[
+
]＞0，即f（x）＞0；
当x＜0时，由偶函数的性质知f（-x）=f（x）＞0；
∴对于定义域A中的任意的x，f（x）≥0，
由f（x）＞m恒成立，得0＞m，
故实数m的取值范围是（-∞，0）．
∴函数f（x）的定义域为（-∞，0）∪（0，+∞），即A=（-∞，0）∪（0，+∞）；
（Ⅱ）由（Ⅰ）知f（x）的定义域关于原点对称，
又f（-x）=-x[
| 1 |
| a |
| 2 |
| a(a-x-1) |
| 1 |
| a |
| 2 |
| a(1-a-x) |
| 1 |
| a |
| 2ax |
| a(ax-1) |
| 1 |
| a |
| 2ax-2+2 |
| a(ax-1) |
| 1 |
| a |
| 2 |
| a(ax-1) |
∴f（x）为偶函数；
（Ⅲ）当x＞0时，∵a＞1，∴ax-1＞0，
∴
| 1 |
| a |
| 2 |
| a(ax-1) |
| 1 |
| a |
| 2 |
| a(ax-1) |
当x＜0时，由偶函数的性质知f（-x）=f（x）＞0；
∴对于定义域A中的任意的x，f（x）≥0，
由f（x）＞m恒成立，得0＞m，
故实数m的取值范围是（-∞，0）．
点评：本题考查函数的奇偶性的判断、定义域的求解，考查函数恒成立问题，考查转化思想，属中档题．
练习册系列答案
相关题目
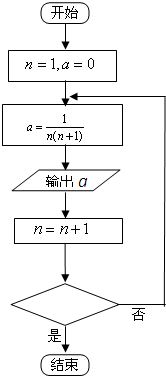执行如图程序框图：