题目内容
14.求过点O(0,0),M(1,1),N(2,4)的圆的方程.分析 设圆的方程是:x2+y2+Dx+Ey+F=0,将三点O(0,0),M1(1,1),M2(2,4)代入方程,求出D,E,F,即可求出圆的方程.
解答 解:设圆的方程是:x2+y2+Dx+Ey+F=0
将三点O(0,0),M1(1,1),M2(2,4)代入方程有:
F=0,且 D+E+F+2=0,且 2D+4E+F+20=0,
∴E=-8,D=6,F=0
所以,圆的方程为:x2+y2+6x-8y=0.
点评 本题考查圆的方程,考查待定系数法,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
9.直线x-y-3=0与圆(x-1)2+y2=2的位置关系( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法判断 |
6.等比数列{an}中,已知a1=3,an=96,其前n顶和Sn=189,则n的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
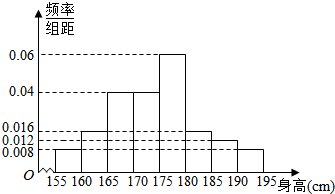 从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.
从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.