Question

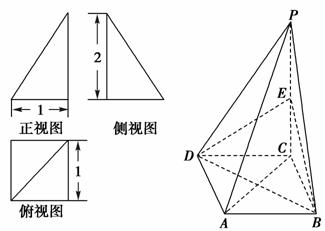
如图，直三棱柱ABC－A₁B₁C₁中，D，E分别是AB，BB₁的中点．

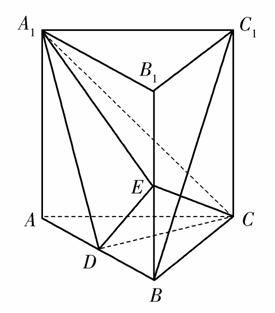
(1)证明：BC₁∥平面A₁CD；

(2)设AA₁＝AC＝CB＝2，AB＝2，求三棱锥C－A₁DE的体积．

Answer 1

[解析]　(1)证明：如图，连结AC₁交A₁C于点F，则F为AC₁中点，又D是AB中点，连结DF，则BC₁∥DF，

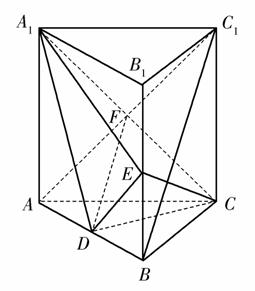
因为DF⊂平面A₁CD，BC₁⊄平面A₁CD，

所以BC₁∥平面A₁CD.

(2)因为ABC－A₁B₁C₁是直三棱柱，所以AA₁⊥CD.由已知AC＝CB，D为AB的中点，所以CD⊥AB.又AA₁∩AB＝A，于是CD⊥平面ABB₁A₁.

由AA₁＝AC＝CB＝2，AB＝2得，

∠ACB＝90°，CD＝，A₁D＝，DE＝，A₁E＝3，

故A₁D²＋DE²＝A₁E²，即DE⊥A₁D

所以VC－A₁DE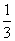＝×(××)×＝1.