题目内容
如图,矩形AMND所在的平面与直角梯形MBCN所在的平面互相垂直,MB∥NC,MN⊥MB.
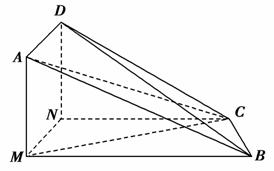
(1)求证:平面AMB∥平面DNC;
(2)若MC⊥CB,求证BC⊥AC.
[证明] (1)因为MB∥NC,MB⊄平面DNC,NC⊂平面DNC,所以MB∥平面DNC.
因为四边形AMND是矩形,所以MA∥DN.
又MA⊄平面DNC,DN⊂平面DNC,
所以MA∥平面DNC.
又MA∩MB=M,且MA、MB⊂平面AMB,
所以平面AMB∥平面DNC.
(2)因为四边形AMND是矩形,所以AM⊥MN.
因为平面AMND⊥平面MBCN,且平面AMND∩平面MBCN=MN,所以AM⊥平面MBCN.
因为BC⊂平面MBCN,所以AM⊥BC.
因为MC⊥BC,MC∩AM=M,所以BC⊥平面AMC.
因为AC⊂平面AMC,所以BC⊥AC.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
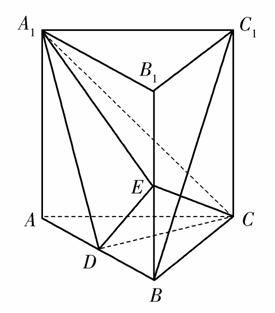
 ,求三棱锥C-A1DE的体积.
,求三棱锥C-A1DE的体积.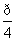 和
和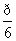 ,过A,B两点分别作两平面交线的垂线,垂足为A′、B′,若AB=12,则A′B′的长为( )
,过A,B两点分别作两平面交线的垂线,垂足为A′、B′,若AB=12,则A′B′的长为( )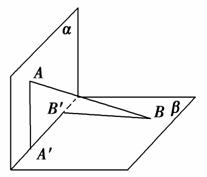
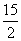 ;
;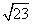 .
.