题目内容
A,B,C是△ABC的内角,向量
=(cos
,sin
),
=(cos
,sin
)满足|
+
|=
(1)求角A的大小
(2)若sinB+sinC=
sinA,试判断△ABC的形状.
| m |
| 3A |
| 2 |
| 3A |
| 2 |
| n |
| A |
| 2 |
| A |
| 2 |
| m |
| n |
| 3 |
(1)求角A的大小
(2)若sinB+sinC=
| 3 |
考点:三角形的形状判断,平面向量数量积的坐标表示、模、夹角
专题:解三角形
分析:(1)根据向量数量积的坐标公式结合两角和差的余弦公式即可求角A的大小
(2)根据正弦定理将条件sinB+sinC=
sinA进行化简,结合余弦定理,求出B,C的大小即可判断△ABC的形状.
(2)根据正弦定理将条件sinB+sinC=
| 3 |
解答:
解:(1)∵
=(cos
,sin
),
=(cos
,sin
)满足|
+
|=
∴|
+
|2=3,
即
2+2
•
+
2=9
即2+2[cos
cos
+sin
sin
]=3,
即2cosA=1,
则cosA=
,
即A=
.
(2)若sinB+sinC=
sinA,
则由正弦定理得b+c=
a,
∵A=
.
∴cosA=
=
=
,
即
=
=
,
即2a2=3bc,
即2sin2A=3sinBsinC,
即sinBsinC=
,
又sinB+sinC=
sinA=
×
=
,
∴sinB=
,sinC=1或sinC=
,sinB=1,
即B=
,C=
或C=
,B=
,
即△ABC是直角三角形.
| m |
| 3A |
| 2 |
| 3A |
| 2 |
| n |
| A |
| 2 |
| A |
| 2 |
| m |
| n |
| 3 |
∴|
| m |
| n |
即
| m |
| m |
| n |
| n |
即2+2[cos
| 3A |
| 2 |
| A |
| 2 |
| 3A |
| 2 |
| A |
| 2 |
即2cosA=1,
则cosA=
| 1 |
| 2 |
即A=
| π |
| 3 |
(2)若sinB+sinC=
| 3 |
则由正弦定理得b+c=
| 3 |
∵A=
| π |
| 3 |
∴cosA=
| b2+c2-a2 |
| 2bc |
| (b+c)2-2bc-a2 |
| 2bc |
| 1 |
| 2 |
即
| 3a2-2bc-a2 |
| 2bc |
| 2a2-2bc |
| 2bc |
| 1 |
| 2 |
即2a2=3bc,
即2sin2A=3sinBsinC,
即sinBsinC=
| 1 |
| 2 |
又sinB+sinC=
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴sinB=
| 1 |
| 2 |
| 1 |
| 2 |
即B=
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
即△ABC是直角三角形.
点评:本题主要考查三角形形状的判断,利用向量数量积的坐标公式以及两角和差的余弦公式将方程进行化简是解决本题的关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知a>b>0,则下列命题正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设x,y满足约束条件
,则目标函数z=
的取值范围为( )
|
| y |
| x+2 |
| A、[-3,3] |
| B、[-3,-2] |
| C、[-2,2] |
| D、[2,3] |
设函数f(x)=sin(
x+θ)-
cos(
x+θ)(|θ|<
),且其图象关于y轴对称,则函数y=f(x)的一个单调递减区间是( )
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
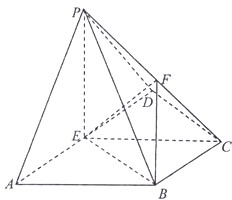 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.