题目内容
已知集合P={(x,y)||x|+|y|≤4},Q={(x,y)|(x-a)2+(y-b)2≤2,a,b∈R}.若Q⊆P,则2a+3b的最大值为( )
| A、4 | B、6 | C、8 | D、12 |
考点:集合的包含关系判断及应用
专题:函数的性质及应用,集合
分析:由题意得到,数对(a,b)满足|a|+|b|≤2,圆心可行域为{(a,b)||a|+|b|≤2}是关键,画出可行域,设设目标函数z=2a+3b,求出目标函数的最大值即可
解答:
 解:∵集合P={(x,y)||x|+|y|≤4},Q={(x,y)|(x-a)2+(y-b)2≤2,a,b∈R},Q⊆P,
解:∵集合P={(x,y)||x|+|y|≤4},Q={(x,y)|(x-a)2+(y-b)2≤2,a,b∈R},Q⊆P,
∴数对(a,b)满足|a|+|b|≤2,
∴圆心可行域为{(a,b)||a|+|b|≤2}
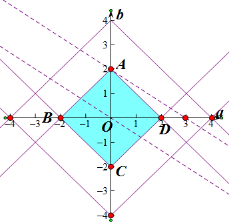
画出圆心的可行域如图所示正方形ABCD所表示的区域,包含边界,
设目标函数z=2a+3b,
则当目标函数过点A(0,2)时,z有最大值,
最大值为2×0+3×2=6
故选:B
 解:∵集合P={(x,y)||x|+|y|≤4},Q={(x,y)|(x-a)2+(y-b)2≤2,a,b∈R},Q⊆P,
解:∵集合P={(x,y)||x|+|y|≤4},Q={(x,y)|(x-a)2+(y-b)2≤2,a,b∈R},Q⊆P,∴数对(a,b)满足|a|+|b|≤2,
∴圆心可行域为{(a,b)||a|+|b|≤2}
画出圆心的可行域如图所示正方形ABCD所表示的区域,包含边界,
设目标函数z=2a+3b,
则当目标函数过点A(0,2)时,z有最大值,
最大值为2×0+3×2=6
故选:B
点评:本题考查了集合,直线与直线,直线和圆的位置关系,绝对值的含义,线性规划,考考查了学生的推理论证能力,运算求解能力,考查了数形结合的思想,分类与整合的思想,函数与方程的思想,等价于转化的思想,属于中档题

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
设函数f(x)=sin(
x+θ)-
cos(
x+θ)(|θ|<
),且其图象关于y轴对称,则函数y=f(x)的一个单调递减区间是( )
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
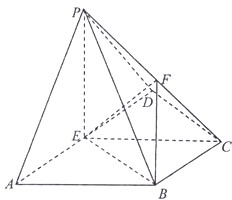 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.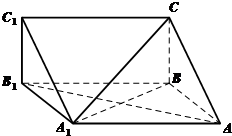 如图,在三棱柱ABC-A1B1C1中,AA1=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.
如图,在三棱柱ABC-A1B1C1中,AA1=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.