Question

定义在R上的函数满足f（x+4）=f（x），且x∈[0，4]时，f（x）=sin

πx

4

，则下列大小关系正确的是（　　）

• A、f（tan1）＜f（

  1

  tan1

  ）
• B、f（cos

  5π

  6

  ）＜f（cos

  π

  3

  ）
• C、f（sin2）＜f（cos2）
• D、f（tan1）＞f（sin1）

Answer 1

考点：抽象函数及其应用

专题：函数的性质及应用

分析：根据函数的周期性画出函数的图象，求出函数在某个区间的单调性，然后利用单调性加以判断，求解即可．

解答： 解：∵定义在R上的函数满足f（x+4）=f（x），
∴f（x）是周期为4的周期函数，
∵x∈[0，4]时，f（x）=sin

πx

4

，
画出函数在[0，4]上的图象，再由周期性得出f（x）的图象，

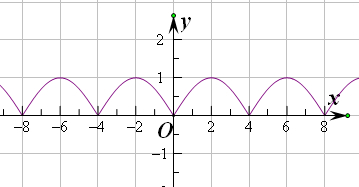
由图象可知，f（x）在[0，2]是单调递增函数，且函数图象关于y轴对称，为偶函数，
A、∵0＜

1

tan1

＜tan1＜2，∴f（tan1）＞f（

1

tan1

），故A错误；
B、∵cos

5π

6

=cos（π-

π

6

）=-cos

π

6

，
∴f（cos

5π

6

）=f（-cos

π

6

）=f（cos

π

6

），
又∵0＜cos

π

3

＜cos

π

6

＜2，
∴f（cos

π

6

）＞f（cos

π

3

）即f（cos

5π

6

）f（cos

π

3

），B错误；
C、f（cos2）=f（-cos2），而0＜-cos2＜sin2＜2所以f（sin2）＞f（cos2），C错误；
D、tan1=

sin1

cos1

＞sin1，且0＜sin1＜tan1＜2，所以f（tan1）＞f（sin1），D正确；
故选：D．

点评：本题主要考查了函数的周期性和单调性和数形结合的思想，属于中档题．