题目内容
函数f(x)=sin(2x-
)在区间[0,
]的值域 .
| π |
| 6 |
| π |
| 3 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:首先利用函数的定义域,进一步利用正弦函数的性质确定函数的值域.
解答:
解:已知:0≤x≤
所以:-
≤2x-
≤
进一步求得:-
≤sin(2x-
)≤1
即函数f(x)的值域为:[-
,1]
故答案为:[-
,1]
| π |
| 3 |
所以:-
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
进一步求得:-
| 1 |
| 2 |
| π |
| 6 |
即函数f(x)的值域为:[-
| 1 |
| 2 |
故答案为:[-
| 1 |
| 2 |
点评:本题考查的知识要点:利用正弦型函数的定义域求函数的值域,函数的图象和性质的应用.属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在R上的函数满足f(x+4)=f(x),且x∈[0,4]时,f(x)=sin
,则下列大小关系正确的是( )
| πx |
| 4 |
A、f(tan1)<f(
| ||||
B、f(cos
| ||||
| C、f(sin2)<f(cos2) | ||||
| D、f(tan1)>f(sin1) |
设x1,x2,x3∈(0,
),a=
,b=
,c=
,且x1>x2>x3,则a,b,c的大小关系为( )
| π |
| 2 |
| 1+sinx1 |
| x1 |
| 1+sinx2 |
| x2 |
| 1+sinx3 |
| x3 |
| A、a>b>c |
| B、c>b>a |
| C、b>c>a |
| D、大小不确定 |
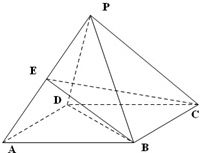 已知四棱锥P-ABCD的底面是正方形,PB=PD,E为PA的中点.
已知四棱锥P-ABCD的底面是正方形,PB=PD,E为PA的中点.