题目内容
8.已知函数f(x)=x2+2x,x∈[-2,1]时的值域为[-1,3].分析 求出函数f(x)的对称轴,得到函数f(x)的最大值和最小值,从而求出函数的值域即可.
解答 解:f(x)=x2+2x=(x+1)2-1,对称轴x=-1,
故函数在[-2,-1)递减,在(-1,1]递增,
故f(x)min=f(-1)=-1,f(x)max=f(1)=3,
故函数的值域是[-1,3],
故答案为:[-1,3].
点评 本题考查了函数的单调性、最值问题,考查二次函数的性质,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.函数f(x)=x2+2x,x∈[-2,1]的值域为( )
| A. | [-1,3] | B. | [4,8] | C. | [1,3] | D. | [2,3] |
17.已知a=log27,b=log20.7,c=20.7,则( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
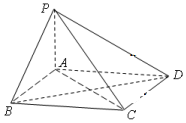 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD