题目内容
15.已知在等比数列{an}中,a1+a2+a3=6,a1+a3+a5=10.5,则公比q( )| A. | -$\frac{1}{2}$或$\frac{3}{2}$ | B. | $\frac{1}{2}$或-$\frac{3}{2}$ | C. | 1或-3 | D. | -1或3 |
分析 设等比数列{an}的公比为q,根据题意可得a1(1+q+q2)=6①与a1(1+q2+q4)=10.5②;进而用②除以①可得$\frac{1+{q}^{2}+{q}^{4}}{1+q+{q}^{2}}$=$\frac{21}{12}$,解可得q的值,即可得答案.
解答 解:根据题意,设等比数列{an}的公比为q,
若a1+a2+a3=6,则a1(1+q+q2)=6,①
a1+a3+a5=10.5,则a1(1+q2+q4)=10.5,②
②÷①可得:$\frac{1+{q}^{2}+{q}^{4}}{1+q+{q}^{2}}$=$\frac{21}{12}$,
变形可得4q(q-1)=3,
解可得q=-$\frac{1}{2}$或$\frac{3}{2}$;
故选:A.
点评 本题考查等比数列的通项公式,注意要利用等比数列通项公式构造关于公比q的方程.

练习册系列答案
相关题目
10.在△ABC中,若$\frac{AC}{AB}$=$\frac{cosB}{cosC}$,则( )
| A. | A=C | B. | A=B | C. | B=C | D. | 以上都不正确 |
18.已知A与B是两个事件,P(B)=$\frac{1}{4}$,P(AB)=$\frac{1}{8}$,则P(A|B)=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
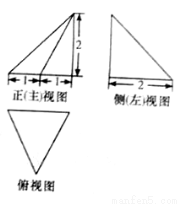
 B.
B. C.
C.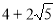 D.
D.