题目内容
9.已知f(x)是定义在R上的偶函数,且在(0,+∞)上是增函数,若f(m-1)-f(2m)<0,则实数m的取值范围是m>$\frac{1}{3}$或m<-1,且m≠1.分析 根据函数奇偶性和单调性的关系中,将不等式进行转化进行求解即可.
解答 解:由f(m-1)<f(2m),
若f(x)是定义在R上的偶函数,且在(0,+∞)上是增函数,
∴不等式等价为f(|m-1|)<f(|2m|),
则|m-1|<|2m|且m≠1,
平方得m2-2m+1<4m2且m≠1,
即3m2+2m-1>0且m≠1,
即m>$\frac{1}{3}$或m<-1,且m≠1,
则实数m的取值范围是m>$\frac{1}{3}$或m<-1,且m≠1,
故答案为:m>$\frac{1}{3}$或m<-1,且m≠1
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系将不等式进行等价转化是解决本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
15.已知在等比数列{an}中,a1+a2+a3=6,a1+a3+a5=10.5,则公比q( )
| A. | -$\frac{1}{2}$或$\frac{3}{2}$ | B. | $\frac{1}{2}$或-$\frac{3}{2}$ | C. | 1或-3 | D. | -1或3 |
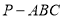 中,
中,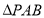 和
和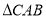 都是以
都是以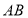 为斜边的等腰直角三角形.
为斜边的等腰直角三角形.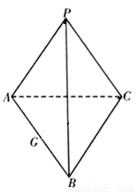
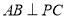 ;
;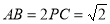 ,求三棱锥
,求三棱锥