题目内容
19.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{9}=1(a>0)$的渐近线为$y=±\frac{3}{4}x$,则该双曲线的离心率为( )| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
分析 求出双曲线的渐近线方程,由题意可得a=4,b=3,求得c,运用离心率公式即可得到所求值.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{9}=1(a>0)$的渐近线方程为y=±$\frac{3}{a}$x,
由渐近线为$y=±\frac{3}{4}x$,可得a=4,
又b=3,可得c=$\sqrt{{a}^{2}+{b}^{2}}$=5,
检验离心率e=$\frac{c}{a}$=$\frac{5}{4}$.
故选:C.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的方程和渐近线方程的关系,以及双曲线的基本量的关系,考查运算能力,属于基础题.

练习册系列答案
相关题目
15.设a>0,则${∫}_{-a}^{a}$$\frac{xdx}{1+cosx}$=( )
| A. | 1 | B. | 0 | C. | 2a | D. | $\frac{3}{4}$a |
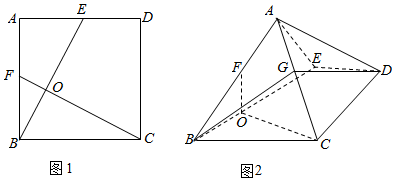 如图1已知正方形ABCD的边长为2,E,F分别为边AD、AB的中点,将△ABE沿BE折起,使平面ABE⊥平面BCDE,如图2,点G为AC的中点
如图1已知正方形ABCD的边长为2,E,F分别为边AD、AB的中点,将△ABE沿BE折起,使平面ABE⊥平面BCDE,如图2,点G为AC的中点