题目内容
11.设集合W由满足下列两个条件的数列{an}构成:①$\frac{{a}_{n}+{a}_{n+2}}{2}<{a}_{n+1}$,②存在实数a、b使a≤an≤b对任意正整数n都成立;(1)现在给出只有5项的有限数列{an},{bn},其中a1=2,a2=6,a3=8,a4=9,a5=12;bk=log2k(k=1,2,3,4,5),试判断数列{an},{bn}是否为集合W的元素;
(2)数列{cn}的前n项和为Sn,c1=1,且对任意正整数n,点(cn+1,Sn)在直线2x+y-2=0上,证明:数列{Sn}∈W,并写出实数a、b的取值范围;
(3)设数列{dn}∈W,且对满足条件②中的实数b的最小值b0,都有dn≠b0(n∈N+),求证:数列{dn}一定是单调递增数列.
分析 (1)由于$\frac{{a}_{3}+{a}_{5}}{2}$=10>9=a4,可知数列{an}不满足条件①.利用对数的运算性质可得:$\frac{{b}_{n}+{b}_{n+2}}{2}$<bn+1,取a=0,b=3,则满足条件②.
(2)由于点(cn+1,Sn)在直线2x+y-2=0上,可得2cn+1+Sn-2=0,利用递推关系可得:cn+1=$\frac{1}{2}{c}_{n}$,利用等比数列的前n项和公式可得:Sn=2$[1-(\frac{1}{2})^{n}]$,验证Sn+Sn+2-2Sn+1<0,可知:条件①成立.由于1≤Sn<2,即可得出条件②及其a,b的范围.
(3)利用反证法:若数列{dn}非单调递增,则一定存在正整数k,使dk≥dk+1 成立,由$\frac{{d}_{m}+{d}_{m+2}}{2}$<dm+1,得 dm+2<2dm+1-dm,变形可得:dm+1>dm+2 .在d1,d2,…,dk这k项中一定存在一个最大值,不妨记为${d}_{{n}_{0}}$=
b0,得出矛盾.
解答 (1)解:∵$\frac{{a}_{3}+{a}_{5}}{2}$=$\frac{8+12}{2}$=10>9=a4,因此数列{an}不满足条件①,∴数列{an}∉W.
∵$\frac{{b}_{n}+{b}_{n+2}}{2}$=$\frac{lo{g}_{2}n+lo{g}_{2}(n+2)}{2}$=$\frac{lo{g}_{2}[n(n+1)]}{2}$<$\frac{lo{g}_{2}(\frac{n+n+2}{2})^{2}}{2}$=log2(n+1)=bn+1,取a=0,b=3,则使a≤bk≤b对k=1,2,3,4,5都成立,
∴数列{bn}∈W.
(2)证明:∵点(cn+1,Sn)在直线2x+y-2=0上,∴2cn+1+Sn-2=0,
当n≥2时,2cn+Sn-1-2=0,可得:2cn+1-2cn+cn=0,化为cn+1=$\frac{1}{2}{c}_{n}$,
∴数列{cn}是等比数列,首项为1,公比为$\frac{1}{2}$.∴Sn=$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$=2$[1-(\frac{1}{2})^{n}]$,
则Sn+Sn+2-2Sn+1=2$[1-(\frac{1}{2})^{n}]$+2$[1-(\frac{1}{2})^{n+2}]$-4$[1-(\frac{1}{2})^{n+1}]$=$2(\frac{1}{2})^{n}$$[2×\frac{1}{2}-1-(\frac{1}{2})^{2}]$<0,
∴$\frac{{S}_{n}+{S}_{n+2}}{2}$<Sn+1.∴条件①成立.
由于1≤Sn<2,∴a≤1,b≥2.
(3)证明::(反证)若数列{dn}非单调递增,则一定存在正整数k,使dk≥dk+1 成立,
当n=m+1时,由$\frac{{d}_{m}+{d}_{m+2}}{2}$<dm+1,得 dm+2<2dm+1-dm,
而dm+1-dm+2>dm+1-(2dm+1-dm)=dm-dm+1≥0,所以dm+1>dm+2 .
显然在d1,d2,…,dk这k项中一定存在一个最大值,不妨记为${d}_{{n}_{0}}$,
所以为${d}_{{n}_{0}}$≥dn(n∈N*),从而为${d}_{{n}_{0}}$=b0.这与题设dn≠b0(n∈N*)相矛盾.
所以假设不成立,故命题得证.
点评 本题考查了等比数列的通项公式前n项和公式、数列的单调性、不等式的性质、反证法、新定义,考查了推理能力与计算能力,属于难题.

| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
| A. | [$\frac{1}{2},\sqrt{2}$) | B. | [$\frac{1}{2},\sqrt{2}$] | C. | [$\frac{\sqrt{2}}{2},\sqrt{2}$) | D. | [$\frac{\sqrt{2}}{2},\sqrt{2}$] |
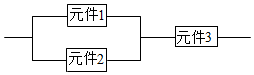 某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1200,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1200小时的概率为$\frac{3}{8}$.
某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1200,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1200小时的概率为$\frac{3}{8}$.