题目内容
8.过点P(3,1)的直线l与圆C:(x-2)2+(y-2)2=4相交于A,B两点,当弦AB的长取最小值时,直线l的倾斜角等于45°.分析 由题意结合图象可得当弦AB的长取最小值时,直线l过P且与PC垂直,由斜率公式和直线的垂直关系可得.
解答 解:∵(3-2)2+(1-2)2=2<4,∴点P在圆C内部,
当弦AB的长取最小值时,直线l过P且与PC垂直,
由斜率公式可得kPC=$\frac{1-2}{3-2}$=-1,
故直线l的斜率为1,倾斜角为45°,
故答案为:45°
点评 本题考查直线和圆的位置关系,涉及直线的倾斜角和斜率以及垂直关系,属基础题.

练习册系列答案
相关题目
4.已知命题p:?x∈R,x-1>lgx,命题q:?x≥0,x≥sinx,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
19.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{9}=1(a>0)$的渐近线为$y=±\frac{3}{4}x$,则该双曲线的离心率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
18.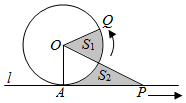 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )| A. | S1=S2 | B. | S1≤S2 | ||
| C. | S1≥S2 | D. | 先S1<S2,再S1=S2,最后S1>S2 |
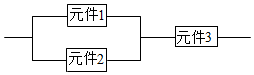 某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1200,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1200小时的概率为$\frac{3}{8}$.
某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1200,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1200小时的概率为$\frac{3}{8}$.