题目内容
9.已知函数f(x)=sin(ωx-$\frac{π}{3}$)(ω>0)图象的相邻的两条对称轴之间的距离为$\frac{π}{2}$(1)求函数f(x)在[0,$\frac{π}{2}$]上的值域;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,已知sinA•sinB+sinB•sinC+cos2B=1且f(C)=0,C∈($\frac{π}{2}$,π),求三边长之比a:b:c.
分析 (1)求出x的系数,根据x的范围,得到2x-$\frac{π}{3}$的范围,从而求出f(x)的最大值和最小值即可;
(2)求出C的值,根据余弦定理求出a,b的关系,从而求出a,b,c的比值即可.
解答 解:(1)函数f(x)=sin(ωx-$\frac{π}{3}$)(ω>0)图象的相邻的两条对称轴之间的距离为$\frac{π}{2}$,
∴$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{π}{2}$,解得:ω=2,
∴f(x)=sin(2x-$\frac{π}{3}$),
当0≤x≤$\frac{π}{2}$时,-$\frac{π}{3}$≤2x-$\frac{π}{3}$≤$\frac{2π}{3}$,
故x=0时,f(x)min=-$\frac{\sqrt{3}}{2}$,当x=$\frac{5π}{12}$时,f(x)max=1,
故所求值域是[-$\frac{\sqrt{3}}{2}$,1];
(2)∵sinA•sinB+sinB•sinC+cos2B=1,
∴sinB(sinA+sinC)=2sin2B,
由sinB≠0,sinA+sinC=sinB,得:a+c=2b,
∵f(c)=0,∴sin(2c-$\frac{π}{3}$)=0,又0<C<π,即-$\frac{π}{3}$<2C-$\frac{π}{3}$<$\frac{5π}{3}$,
∴C=$\frac{π}{6}$或C=$\frac{2π}{3}$,∵C∈($\frac{π}{2}$,π),
∴C=$\frac{π}{6}$,
由余弦定理得:
cosC=$\frac{{a}^{2}{+b}^{2}{-(2b-a)}^{2}}{2ab}$=$\frac{4a-3b}{2a}$,
当C=$\frac{2π}{3}$时,$\frac{4a-3b}{2a}$=-$\frac{1}{2}$,
∴5a=3b,此时:a:b:c=3:5:7,
故所求三边之比是:3:5:7.
点评 本题考查了正弦定理、余弦定理的应用,考查三角函数问题,是一道中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -$\frac{3}{2}$或-2 | D. | $\frac{3}{2}$或-2 |
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
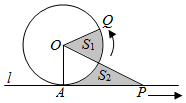 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )| A. | S1=S2 | B. | S1≤S2 | ||
| C. | S1≥S2 | D. | 先S1<S2,再S1=S2,最后S1>S2 |
| A. | 16 | B. | 17 | C. | 40 | D. | 41 |