题目内容
15.在正项等比数列{an}中,${a_2}=8,\;\;16{a_4}^2={a_1}•{a_5}$,则等比数列{an}的前n项积Tn中最大的值是( )| A. | T3 | B. | T4 | C. | T5 | D. | T6 |
分析 由题意可得数列的首项和公比,由等差数列的求和公式可得Tn,由二次函数的最值可得.
解答 解:∵在正项等比数列{an}中${a_2}=8,\;\;16{a_4}^2={a_1}•{a_5}$,
∴16a42=a1a5=a32,∴16a32q2=a32,解得q=$\frac{1}{4}$,
∴a1=$\frac{{a}_{2}}{q}$=$\frac{8}{\frac{1}{4}}$=32,
∴等比数列{an}的前n项积Tn=a1nq1+2+…+n-1
=32n•$(\frac{1}{4})^{\frac{(n-1)(1+n-1)}{2}}$=25n•${2}^{n-{n}^{2}}$=${2}^{6n-{n}^{2}}$,
由二次函数可知当n=-$\frac{6}{2×(-1)}$=3时,Tn取最大的值.
故选:A.
点评 本题考查等比数列的求和公式和等差数列的求和公式,涉及二次函数的最值,属基础题.

练习册系列答案
相关题目
3.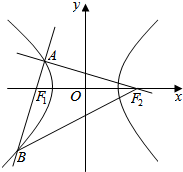 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )
 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )| A. | $\sqrt{5+2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{4-2\sqrt{2}}$ |
10.已知点P是抛物线y2=2x上的一个动点,则点P到点D$(2,\frac{3}{2}\sqrt{3})$的距离与点P到y轴的距离之和的最小值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
7.命题“存在x0∈R使得2${\;}^{{x}_{0}}$≤1”的否定是( )
| A. | 不存在x0∈R使得2${\;}^{{x}_{0}}$>0 | B. | 存在x0∈R使得2${\;}^{{x}_{0}}$>0 | ||
| C. | 对任意x∈R,2x>0 | D. | 对任意x∈R,2x≤0 |
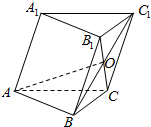 已知斜三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,∠BAA1=$\frac{2π}{3}$,∠CAA1=$\frac{π}{3}$,AB=AC=1,AA1=2,点O是B1C与BC1的交点.
已知斜三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,∠BAA1=$\frac{2π}{3}$,∠CAA1=$\frac{π}{3}$,AB=AC=1,AA1=2,点O是B1C与BC1的交点.