题目内容
5.已知函数f(x)=sin$\frac{x}{2}$+$\sqrt{3}$cos$\frac{x}{2}$,x∈R.(1)求函数f(x)的最小正周期;
(2)求函数f(x)在x∈[-2π,2π]上的单调递增区间.
分析 (1)化简可得f(x)=2sin($\frac{x}{2}$+$\frac{π}{3}$),由周期公式可得;
(2)解2kπ-$\frac{π}{2}$≤$\frac{x}{2}$+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$可得函数的单调递增区间,取x∈[-2π,2π]上部分的即可.
解答 解:(1)化简可得f(x)=sin$\frac{x}{2}$+$\sqrt{3}$cos$\frac{x}{2}$=2sin($\frac{x}{2}$+$\frac{π}{3}$),
∴函数f(x)的最小正周期T=$\frac{2π}{\frac{1}{2}}$=4π;
(2)由2kπ-$\frac{π}{2}$≤$\frac{x}{2}$+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$可得4kπ-$\frac{5π}{3}$≤x≤4kπ+$\frac{π}{3}$,k∈Z.
∴函数f(x)的单调递增区间为[4kπ-$\frac{5π}{3}$,4kπ+$\frac{π}{3}$],k∈Z,
由x∈[-2π,2π]可得单调递增区间为[-$\frac{5π}{3}$,$\frac{π}{3}$].
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和单调性,属基础题.

练习册系列答案
相关题目
15.函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},x≥2}\\{{2}^{x},x<1}\end{array}\right.$的值域为( )
| A. | (-∞,+∞) | B. | (0,+∞) | C. | (0,2)∪[$\frac{5}{2}$,+∞) | D. | (-∞,2)∪[$\frac{5}{2}$,+∞) |
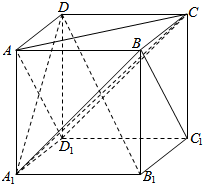 如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )
如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )