题目内容
若存在区间[m,n],使得函数f(x)定义域为[m,n]时,其值域为[km,kn](k∈N*),则称区间[m,n]为函数f(x)的“k倍区间”.已知函数f(x)=x3+sinx,则f(x)的“5倍区间”的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:函数的值域
专题:新定义
分析:由函数f(x)的“k倍区间”的定义,结合函数f(x)=x3+sinx的单调性,即可得到函数f(x)的“5倍区间”的个数.
解答:
解:令f(x)=5x,求y=f(x)-5x,y′=3x2-5+cosx,
令y′=0,抛物线y=x2-5与y=cosx只有两个交点,且x=±a,1.3<a<1.4,a<
,
y=x3+sinx-5x在(-∞,-a)是增函数,(-a,a)是减函数,(a,+∞)是增函数,
则函数y=x3+sinx-5x的极大值是(-a)3+sin(-a)+5a>0,极小值是a3+sina-5a<0,
∴f(x)-5x=0有3根,∴y=f(x)与y=5x有3个公共点.
故选:D.
令y′=0,抛物线y=x2-5与y=cosx只有两个交点,且x=±a,1.3<a<1.4,a<
| π |
| 2 |
y=x3+sinx-5x在(-∞,-a)是增函数,(-a,a)是减函数,(a,+∞)是增函数,
则函数y=x3+sinx-5x的极大值是(-a)3+sin(-a)+5a>0,极小值是a3+sina-5a<0,
∴f(x)-5x=0有3根,∴y=f(x)与y=5x有3个公共点.
故选:D.
点评:本题考查新定义,主要考查函数的考查函数单调性的应用,体现了转化的数学思想,正确理解新定义是关键,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知函数f(x)(x∈R)满足f(2)=9,且f(x)的导函数f′(x)<
,则f(x)<x3+
x的解集为( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、{x|-2<x<2} |
| B、{x|x<-2} |
| C、{x|x<-2或x>2} |
| D、{x|x>2} |
等差数列{an}的前n项和为Sn,且9a1,3a2,a3成等比数列,若a1=3,则a4等于( )
| A、6 | B、4 | C、3 | D、5 |
设函数f(x)的定义域是R,若f(1-x)=f(1+x),且当x≥1时,f(x)=-
x3-2x+1,则有( )
| 1 |
| 3 |
A、f(
| ||||||
B、f(
| ||||||
C、f(
| ||||||
D、f(
|
在△ABC中,三个内角A、B、C成等差数列,则角A+C=( )
| A、30° | B、60° |
| C、90° | D、120° |
已知函数y=
,则直线y=x+1与函数图象交点的个数是( )
| 1+x|x| |
| A、0 | B、1 | C、2 | D、3 |
复数
(i为虚数单位)的模为( )
| 2+i |
| i |
A、
| ||
| B、±(1-2i) | ||
C、
| ||
| D、1-2i |
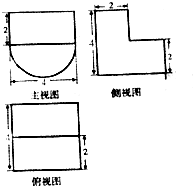
某几何体的三视图如图所示,则该几何体的表面积为( )

| A、40+12π |
| B、16+8π |
| C、16+16π |
| D、16+32π |