题目内容
已知函数f(x)(x∈R)满足f(2)=9,且f(x)的导函数f′(x)<
,则f(x)<x3+
x的解集为( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、{x|-2<x<2} |
| B、{x|x<-2} |
| C、{x|x<-2或x>2} |
| D、{x|x>2} |
考点:导数的运算
专题:
分析:令g(x)=f(x)-x3-
x,从而可得g(x)的单调性,结合f(2)=9,可求得g(2)=0,然后求出不等式的解集即可
| 1 |
| 2 |
解答:
解:∵f(x)<x3+
x,
∴f(x)-x3-
x<0,
令g(x)=f(x)-x3-
x,
∴g′(x)=f′(x)-3x2-
,
∵f′(x)<
,
∴g′(x)<0,
∴g(x)在R上是单调递减的,
∵g(2)=f(2)-23-
×2=0,
∴g(x)<0的解集是x>2.
故选:D.
| 1 |
| 2 |
∴f(x)-x3-
| 1 |
| 2 |
令g(x)=f(x)-x3-
| 1 |
| 2 |
∴g′(x)=f′(x)-3x2-
| 1 |
| 2 |
∵f′(x)<
| 1 |
| 2 |
∴g′(x)<0,
∴g(x)在R上是单调递减的,
∵g(2)=f(2)-23-
| 1 |
| 2 |
∴g(x)<0的解集是x>2.
故选:D.
点评:本题利用导数研究函数的单调性,可构造函数,考查所构造的函数的单调性是关键,也是难点所在,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
向量
=(1,2),
=(1,-λ),在区间[-5,5]上随机取一个数λ,使向量2
+
与
-
的夹角为锐角的概率为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,BC=3,AC=
,B=
,则△ABC的面积是( )
| 13 |
| π |
| 3 |
A、3
| ||||
B、6
| ||||
C、
| ||||
D、
|
若存在区间[m,n],使得函数f(x)定义域为[m,n]时,其值域为[km,kn](k∈N*),则称区间[m,n]为函数f(x)的“k倍区间”.已知函数f(x)=x3+sinx,则f(x)的“5倍区间”的个数是( )
| A、0 | B、1 | C、2 | D、3 |
(3x-
)n的展开式中各项系数之和为A,所有偶数项的二项式系数为B,若A+B=96,则展开式中的含有x2的项的系数为( )
| 1 | |||
|
| A、-540 | B、-180 |
| C、540 | D、180 |
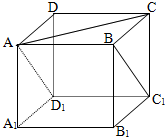 如图,正方体ABCD-A1B1C1D1中,点P是直线BC1的动点,则下列四个命题:
如图,正方体ABCD-A1B1C1D1中,点P是直线BC1的动点,则下列四个命题: