题目内容
 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2| 2 |
(1)证明:平面ABC⊥平面ADC;
(2)若∠BDC=60°,求直线BM与CD所成的余弦值的大小.
(3)若∠BDC=60°,求二面角C-BM-D的大小.
考点:二面角的平面角及求法,异面直线及其所成的角,平面与平面垂直的判定
专题:空间角
分析:(1)由已知条件推导出BC⊥AD,从而得到BC⊥平面ACD,由此能够证明平面ABC⊥平面ADC.
(2)取AC中点N,连结MN,BN,由已知条件推导出∠NMB是直线BM与CD所成的角,由此能求出直线BM与CD所成的余弦值.
(3)作CG⊥BD于G,作GH⊥BM于旧H,连结HG,CH,由已知条件推导出∠CHG为二面角的平面角,由此能求出二面角C-BM-D的大小.
(2)取AC中点N,连结MN,BN,由已知条件推导出∠NMB是直线BM与CD所成的角,由此能求出直线BM与CD所成的余弦值.
(3)作CG⊥BD于G,作GH⊥BM于旧H,连结HG,CH,由已知条件推导出∠CHG为二面角的平面角,由此能求出二面角C-BM-D的大小.
解答:
(1)证明:∵AD⊥平面BCD,BC?平面BCD,∴BC⊥AD,
又∵BC⊥CD,AD∩CD=D,∴BC⊥平面ACD,
又∵BC?平面ABC,∴平面ABC⊥平面ADC.
(2)解: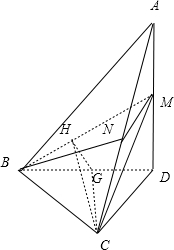 取AC中点N,连结MN,BN,
取AC中点N,连结MN,BN,
∵M是AD中点,∴MN∥DC,
∴∠NMB是直线BM与CD所成的角,
∵AD⊥平面BCD,BC⊥CD,AD=2,BD=2
,
∴CD=
,BC=
=
,AC=
=
,AB=
=2
,
∴cos∠BCA=
=0,∴∠BCA=90°,
∴BN=
=
=
,MN=
CD=
,
BM=
=
=3,
∴cos∠NMB=
=
.
∴直线BM与CD所成的余弦值为
.
(3)解:作CG⊥BD于G,作GH⊥BM于旧H,连结HG,CH,
∵AD⊥平面BCD,CG?平面BCD,∴CG⊥AD,
又∵CG⊥BD,AD∩BD=D,∴CG⊥平面ABD,
又∵BM?平面ABD,∴BM⊥CG,
又∵BM⊥CH,CG∩GH=G,∴BM⊥平面CGH,
∵CH?平面CGH∴BM⊥CH,
∴∠CHG为二面角的平面角.
在Rt△BCD中,
CD=BDcos60°=
,CG=CDsin60°=
,BG=BCsin60°=
在Rt△BDM中,HG=
=
在Rt△CHG中,tan∠CHG=
=
=
∴∠CHG=60°,即二面角C-BM-D的大小为60°.
又∵BC⊥CD,AD∩CD=D,∴BC⊥平面ACD,
又∵BC?平面ABC,∴平面ABC⊥平面ADC.
(2)解:
 取AC中点N,连结MN,BN,
取AC中点N,连结MN,BN,∵M是AD中点,∴MN∥DC,
∴∠NMB是直线BM与CD所成的角,
∵AD⊥平面BCD,BC⊥CD,AD=2,BD=2
| 2 |
∴CD=
| 2 |
| 8-2 |
| 6 |
| 4+2 |
| 6 |
| 4+8 |
| 3 |
∴cos∠BCA=
| 6+6-12 |
| 2×6 |
∴BN=
| BC2+CN2 |
6+
|
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
BM=
| BD2+DM2 |
| 8+1 |
∴cos∠NMB=
9+
| ||||
2×3×
|
| ||
| 3 |
∴直线BM与CD所成的余弦值为
| ||
| 3 |
(3)解:作CG⊥BD于G,作GH⊥BM于旧H,连结HG,CH,
∵AD⊥平面BCD,CG?平面BCD,∴CG⊥AD,
又∵CG⊥BD,AD∩BD=D,∴CG⊥平面ABD,
又∵BM?平面ABD,∴BM⊥CG,
又∵BM⊥CH,CG∩GH=G,∴BM⊥平面CGH,
∵CH?平面CGH∴BM⊥CH,
∴∠CHG为二面角的平面角.
在Rt△BCD中,
CD=BDcos60°=
| 2 |
| ||
| 2 |
3
| ||
| 2 |
在Rt△BDM中,HG=
| BG?DM |
| BM |
| ||
| 2 |
在Rt△CHG中,tan∠CHG=
| CG |
| HG |
| ||||
|
| 3 |
∴∠CHG=60°,即二面角C-BM-D的大小为60°.
点评:本题考查平面与平面垂直的证明,考查直线与直线所成角的余弦值的求法,考查二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AB⊥AD,平面PAD⊥平面ABCD,若AB=8,DC=2,AD=6
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AB⊥AD,平面PAD⊥平面ABCD,若AB=8,DC=2,AD=6 甲、乙两个学习小组各有10名同学,他们在一次数学测验中的成绩可用如图的茎叶图表示.则在这次测验中成绩较好的是
甲、乙两个学习小组各有10名同学,他们在一次数学测验中的成绩可用如图的茎叶图表示.则在这次测验中成绩较好的是