题目内容

（1）已知y=|2x-2|，用“列表、描点、连线”的方式画出函数图象．
（2）已知 y=f（x）图象，试根据图象求函数解析式．
考点：函数的图象,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：（1）先化为分段函数，再列表，描点，连线即可．
（2）由图象可设设函数解析式y=a（x+1）（x-4），又过点（0，-4），解得即可．
解答： 解：（1）∵y=|2x-2|=
2x-2，x≥1
2-2x，x＜1
，
列表得
x…012…
y…202…
描点，连线，图象如图所示

解（2）：设函数解析式y=a（x+1）（x-4），
将（0，-4）代入得-4=a（0+1）（0-4），
解得a=1
所以，函数解析式y=（x+1）（x-4），
点评：本题主要考查了函数的图象的画法和二次函数的解析式的求法，属于基础题．
练习册系列答案
相关题目
已知命题p：若x2+y2=0，则x、y全为0；命题q：若a＞b，则
1
a
＜
1
b
．给出下列四个复合命题：①p且q，
②p或q，③?p④?q，其中是命题的是
 
．
已知①
5
∈R；②
1
3
∈Q；③0={0}； ④0∉N；⑤π∈Q其中正确的有
 
．
已知幂函数f（x）=x(m2+m)-1（m∈N*），经过点（2，
2
），试确定m的值，并求满足条件f（2-a）＞f（a-1）的实数a的取值范围．
定义在R上的奇函数f（x）满足：f（2）=0，f（x）=f（x+3），求f（x）=0在x∈[0，3]上的解
 
．
已知sinα=
4
5
，α∈（
π
2
，π），cosβ=-
5
13
，β是第三象限角，则sin（α+β）=
 
．
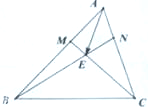在△ABC中，已知AM：AB=1：3，AN：AC=1：4，BN与CM交于点E，
AB
=
a
，
AC
=
b
，则
AE
=
 
（用
a
，
b
表示
AE
）．
关于x的不等式ax2+bx+c≥0的解集是{x|-
1
2
≤x≤
1
3
}，则
b
c
=
 
．
设函数f（x）=
x2+1，x≤1
1
x
，x＞1
则f（f（3））=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网