题目内容
15.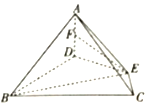 如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.(1)若F是AD的中点,求证:EF∥平面ABC;
(2)M、N是棱BC的两个三等分点,求证:EM⊥平面ADN.
分析 (1)取BD的中点G,连接EG,FG,证明平面EFG∥平面ABC,即可证明:EF∥平面ABC;
(2)M、N是棱BC的两个三等分点,证明EM⊥ND,AD⊥EM,即可证明:EM⊥平面ADN.
解答 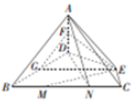 证明:(1)取BD的中点G,连接EG,FG,
证明:(1)取BD的中点G,连接EG,FG,
∵F是AD的中点,
∴FG∥AB,
∵BD=2CE,∴BG=CE,
∵∠DBC=∠BCE,
∴E,G到直线BC的距离相等,则EG∥CB,
∵EG∩FG=G,
∴平面EFG∥平面ABC,
∵EF?平面EFG,
∴EF∥平面ABC;
(2)∵BD⊥DE,∠DBC=∠BCE═60°,BD=2CE,
∴BC=3CE,
∵M、N是棱BC的两个三等分点,
∴MN=CE,BD=BN,
∵∠DBC=60°,
∴△BDN是正三角形,即∠BND=60°,
∵∠BCE=60°,∴CE∥ND,
△CEM中,CM=2CE,∠BCE=60°,
∴∠CEM=90°,
∴EM⊥CE,EM⊥ND,
∵AD⊥平面BCED,
∴AD⊥EM,
∵AD∩ND=D,
∴EM⊥平面ADN.
点评 本题考查面面平行、线面平行的判定,考查线面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.若关于x的方程x2-xlnx+2=k(x+2)在[$\frac{1}{2}$,+∞)上有两解,则实数k的取值范围为( )
| A. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$] | B. | (1,+∞) | C. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$) | D. | [1,+∞) |
6.在复平面内,复数z=$\frac{2i}{1+i}$(i为虚数单位)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知函数f(x)=-x2-6x-3,g(x)=2x3+3x2-12x+9,m<-2,若?x1∈[m,-2),?x2∈(0,+∞),使得f(x1)=g(x2)成立,则m的最小值为( )
| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |
20.设集合A={x∈R|x-1>0},B={x∈R|x<0},C={x∈R|x(x-2)>0},则“x∈A∪B“是“x∈C“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
7.设M、N是直线x+y-2=0上的两动点,且|MN|=$\sqrt{2}$,则$\overrightarrow{OM}$•$\overrightarrow{ON}$的最小值为( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
5.设集合A={x|x2-3x<0},B={x||x|>2},则A∩B=( )
| A. | (2,3) | B. | (-2,3) | C. | (0,2) | D. | (-2,0) |