题目内容
4.若数列{an}满足:只要ap=aq(p,q∈N*),必有ap+1=aq+1,那么就称数列{an}具有相纸P,已知数列{an}具有性质P,且a1=1,a2=2,a3=3,a5=2,a6+a7+a8=21,则a2017=15.分析 根据题意,由于数列{an}具有性质P以及a2=a5=2,分析可得a3=a6=3,a4=a7,a5=a8=3,结合题意可以将a6+a7+a8=21变形为a3+a4+a5=21,计算可得a4的值,进而分析可得a3=a6=a9=…a3n=3,a4=a7=a6=…a3n+1=15,a5=a8=…a3n+2=3,(n≥1);分析可得a2017的值.
解答 解:根据题意,数列{an}具有性质P,且a2=a5=2,
则有a3=a6=3,a4=a7,a5=a8=3,
若a6+a7+a8=21,可得a3+a4+a5=21,则a4=21-3-3=15,
进而分析可得:a3=a6=a9=…a3n=3,a4=a7=a6=…a3n+1=15,a5=a8=…a3n+2=3,(n≥1)
则a2017=a3×672+1=15,
故答案为:15.
点评 本题考查数列的表示方法,关键分析什么样的数列具有性质P,并且求出a4的值,

练习册系列答案
相关题目
14.已知z1与z2是共轭虚数,有4个命题①z12<|z2|2; ②z1z2=|z1z2|;③z1+z2∈R;④$\frac{{z}_{1}}{{z}_{2}}$∈R,一定正确的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②③ |
19.设复数z1,z2在复平面内的对应点关于虚轴对称,若z1=1-2i,其中i是虚数单位,则$\frac{{z}_{2}}{{z}_{1}}$的虚部为( )
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$i | D. | $\frac{4}{5}$i |
9.设数列{an}是各项为正数的等比数列,Sn为其前n项和,已知a2a4=16,$\frac{{a}_{4}+{a}_{5}+{a}_{8}}{{a}_{1}+{a}_{2}+{a}_{5}}$=8,则S5=( )
| A. | 40 | B. | 20 | C. | 31 | D. | 43 |
16.已知实数集R,集合$M=\left\{{x|{{log}_3}x<3}\right\},N=\left\{{x|{x^2}-4x-5>0}\right\}$,则M∩(∁RN)=( )
| A. | [-1,8) | B. | (0,5] | C. | [-1,5) | D. | (0,8) |
13.复数z满足z=i(1-i),则$\overline{z}$等于( )
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
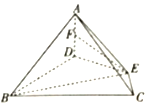 如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.