题目内容
5.设集合A={x|x2-3x<0},B={x||x|>2},则A∩B=( )| A. | (2,3) | B. | (-2,3) | C. | (0,2) | D. | (-2,0) |
分析 求出集合A,B,利用集合的基本运算即可得到结论.
解答 解:A={x|x2-3x<0}=(0,3),B={x||x|>2}={x|x>2或x<-2}=(-∞,-2)∪(2,+∞),
则A∩B=(2,3)
故选:A
点评 本题主要考查集合的基本运算,利用不等式求出对应的集合是解决本题的关键,比较基础.

练习册系列答案
相关题目
16.已知实数集R,集合$M=\left\{{x|{{log}_3}x<3}\right\},N=\left\{{x|{x^2}-4x-5>0}\right\}$,则M∩(∁RN)=( )
| A. | [-1,8) | B. | (0,5] | C. | [-1,5) | D. | (0,8) |
13.复数z满足z=i(1-i),则$\overline{z}$等于( )
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
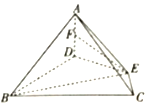 如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.