题目内容

3．已知函数f（x）=-x2-6x-3，g（x）=2x3+3x2-12x+9，m＜-2，若?x1∈[m，-2），?x2∈（0，+∞），使得f（x1）=g（x2）成立，则m的最小值为（　　）
A．-5B．-4C．-2$\sqrt{5}$D．-3

分析 利用导数先求出函数g（x）的最小值，再根据函数f（x）的图象和性质，即可求出m的最小值

解答 解：∵g（x）=2x3+3x2-12x+9，
∴g′（x）=6x2+6x-12=6（x+2）（x-1），
则当0＜x＜1时，g′（x）＜0，函数g（x）递减，
当x＞1时，g′（x）＞0，函数g（x）递增，
∴g（x）min=g（1）=2，
∵f（x）=-x2-6x-3=-（x+3）2+6≤6，
作函数y=f（x）的图象，如图所示，
当f（x）=2时，方程两根分别为-5和-1，
则m的最小值为-5，
故选：A

点评 本题主要考查了了函数的值域，根据函数值域之间的关系是解决本题的关键．

练习册系列答案
相关题目
13．设O是坐标原点，AB是圆锥曲线的一条不经过点O且不垂直于坐标轴的弦，M是弦AB的中点，KAB，KOM分别表示直线AB，OM的斜率，在圆x2+y2=r2中，KAB•KOM=-1，在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）中，类比上述结论可得若AB是圆锥曲线的一条不经过点O且不垂直于坐标轴的弦，M是弦AB的中点，则${K_{AB}}•{K_{OM}}=-\frac{b^2}{a^2}$．
14．已知z1与z2是共轭虚数，有4个命题①z12＜|z2|2； ②z1z2=|z1z2|；③z1+z2∈R；④$\frac{{z}_{1}}{{z}_{2}}$∈R，一定正确的是（　　）
A．①②B．②③C．③④D．①②③
11．设M，N是直线x+y-2=0上的两点，若M（1，1），且|MN|=$\sqrt{2}$，则$\overrightarrow{OM}$•$\overrightarrow{ON}$的值为（　　）
A．1B．2C．3D．4
18．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=4-t}\end{array}\right.$（t为参数），在以O为极点x轴的非负半轴为极轴建立的极坐标系中，曲线C的极坐标方程为ρ=2．
（1）求直线l的普通方程和曲线C的直角坐标方程；
（2）若点Q是曲线C上的动点，求点Q到直线l的距离的最大值．
8．已知抛物线C：y2=2px（p＞0）的焦点为F，点M（x0，2$\sqrt{2}$）是抛物线C上一点，圆M与y轴相切且与线段MF相交于点A，若$\frac{|MA|}{|AF|}$=2，则p等于（　　）
A．1B．2C．2$\sqrt{2}$D．4
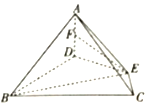15．如图，在四棱锥A-BCED中，AD⊥底面BCED，BD⊥DE，∠DBC=∠BCE═60°，BD=2CE．
（1）若F是AD的中点，求证：EF∥平面ABC；
（2）M、N是棱BC的两个三等分点，求证：EM⊥平面ADN．
12．在△ABC中，角A，B，C所对边分别是a，b，c，若sin（A-B）=$\frac{a}{a+b}$sinAcosB-$\frac{b}{a+b}$sinBcosA．
（1）求证：A=B；
（2）若A=$\frac{7π}{24}$，a=$\sqrt{6}$，求△ABC的面积．
13．复数z满足z=i（1-i），则$\overline{z}$等于（　　）
A．-1+iB．-1-iC．1-iD．1+i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网