题目内容
已知函数f(x)为偶函数,且当x≥0时,f(x)=2x-a,且f(-2)=3,
(1)求f(x)的解析式;
(2)求满足f(x)>1的x的取值范围.
(1)求f(x)的解析式;
(2)求满足f(x)>1的x的取值范围.
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)利用偶函数的定义f(-x)=f(x),先求出a的值,把x≤0转化为-x≥0,再利用x≥0时,f(x)=2-x-1.
(2)需要分类讨论,即可求出不等式的解集.
(2)需要分类讨论,即可求出不等式的解集.
解答:
解:(1)∵函数f(x)是定义域为R上的偶函数,
∴f(-x)=f(x),
∴f(-2)=f(2),
∵x≥0时,f(x)=2x-a,f(-2)=3
∴22-a=3,
解得a=1,
∴x≥0时,f(x)=2x-1,
令x<0则-x>0,
∴f(-x)=2-x-1=(
)x-1=f(x)
即x<0时f(x)=(
)x-1=
故f(x)=
,
(2)当x≥0时,f(x)>1,
∴2x-1>1,
解得,x>1,
当x<0时,f(x)>1,
∴2-x-1>1,
解得-2<x<0,
综上所述不等式的解集为(-2,0)∪(1,+∞)
∴f(-x)=f(x),
∴f(-2)=f(2),
∵x≥0时,f(x)=2x-a,f(-2)=3
∴22-a=3,
解得a=1,
∴x≥0时,f(x)=2x-1,
令x<0则-x>0,
∴f(-x)=2-x-1=(
| 1 |
| 2 |
即x<0时f(x)=(
| 1 |
| 2 |
故f(x)=
|
(2)当x≥0时,f(x)>1,
∴2x-1>1,
解得,x>1,
当x<0时,f(x)>1,
∴2-x-1>1,
解得-2<x<0,
综上所述不等式的解集为(-2,0)∪(1,+∞)
点评:本题考查了函数的解析式的求法,函数的奇偶性,以及不等式的解法,属于基础题

练习册系列答案
相关题目
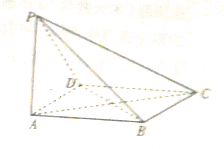 如图,四边形ABCD是菱形,PA⊥ABCD,AD=2,∠BAD=60°.
如图,四边形ABCD是菱形,PA⊥ABCD,AD=2,∠BAD=60°.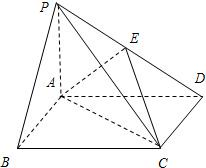 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4.E是PD的中点,
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4.E是PD的中点,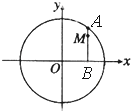 如图,设A是圆x2+y2=6上的动点,点B是A在x轴上投影,M为AB上一点,且|MB|=
如图,设A是圆x2+y2=6上的动点,点B是A在x轴上投影,M为AB上一点,且|MB|=