题目内容
已知数列{an}的前n项和公式为Sn=
×3n+1-
.
(1)求数列{an}的通项公式;
(2)令bn=log3
,求数列 {|bn|}的前n项和Tn(其中,n≥5).
| 1 |
| 2 |
| 3 |
| 2 |
(1)求数列{an}的通项公式;
(2)令bn=log3
| an |
| 81 |
考点:数列的求和,数列的函数特性
专题:函数的性质及应用,等差数列与等比数列
分析:(1)利用an=
求解.
(2)bn=log3
=log3
=n-4,由此能求出数列 {|bn|}的前n项和Tn(其中,n≥5).
|
(2)bn=log3
| an |
| 81 |
| 3n |
| 81 |
解答:
解:(1)∵Sn=
×3n+1-
,
∴当n=1时,a1=S1=
×32-
=3,
当n≥2时,an=Sn-Sn-1=(
×3n+1-
)-(
×3n+2-
)=3n,
当n=1时,上式成立,
∴an=3n.
(2)bn=log3
=log3
=n-4,
令bn≥0,即n-4≥0,得n≥4,
即第四项开始各项均非负,
∴当n≥5时,Tn=3+2+1+0+
=
n2-
n+12.
| 1 |
| 2 |
| 3 |
| 2 |
∴当n=1时,a1=S1=
| 1 |
| 2 |
| 3 |
| 2 |
当n≥2时,an=Sn-Sn-1=(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当n=1时,上式成立,
∴an=3n.
(2)bn=log3
| an |
| 81 |
| 3n |
| 81 |
令bn≥0,即n-4≥0,得n≥4,
即第四项开始各项均非负,
∴当n≥5时,Tn=3+2+1+0+
| (n-4)[1+(n-4)] |
| 2 |
=
| 1 |
| 2 |
| 7 |
| 2 |
点评:本题考查数列的通项公式和前n项绝对值的和的求法,解题时要注意对数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面四个推导过程符合演绎推理三段论形式且推理正确的是( )
| A、大前提:无限不循环小数是无理数;小前提:π丌是无理数;结论:π是无限不循环小数 |
| B、大前提:无限不循环小数是无理数;小前提:π是无限不循环小数;结论:π是无理数 |
| C、大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论:π是无理数 |
| D、大前提:π是无限不循环小数;小前提:π是无理数;结论:无限不循环小数是无理数 |
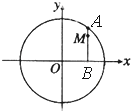 如图,设A是圆x2+y2=6上的动点,点B是A在x轴上投影,M为AB上一点,且|MB|=
如图,设A是圆x2+y2=6上的动点,点B是A在x轴上投影,M为AB上一点,且|MB|=