题目内容
在等腰直角三角形ABC中，CA=CB=3，平面内一点M满足
=λ
（λ≥2，λ∈R），则
•
的最大值为 ．
| BM |
| AM |
| CM |
| CA |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：先根据向量数量积的几何意义，将
•
表示为|
|乘以向量
在
方向上的射影，只需射影最大即可，由λ≥2知，当λ=2时，|
|最大，则
•
最大，再设法求出射影|
|cos∠MCA，即可得
•
的最大值．
| CM |
| CA |
| CA |
| CM |
| CA |
| AM |
| CM |
| CA |
| CM |
| CM |
| CA |
解答：
解：∵CA=3，∴
•
=|
|•(|
|cos∠MCA)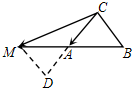
=3(|
|cos∠MCA)，
其中|
|cos∠MCA为向量
在
方向上的射影．
如右图所示，当|
|越大，射影|
|cos∠MCA也越大，
由λ≥2知，当M往左移到最远处，即λ=2时，|
|最大，则
•
最大，
此时点A为线段BM的中点．
过点M作MD⊥CA交CA的延长线于点D，则
由
，知△MDA≌△BCA，
∴AD=CA，
∴
•
的最大值=3|
|=3×2|
|=6×3=18．
故答案为18．
| CM |
| CA |
| CA |
| CM |
=3(|
| CM |
其中|
| CM |
| CM |
| CA |
如右图所示，当|
| AM |
| CM |
由λ≥2知，当M往左移到最远处，即λ=2时，|
| AM |
| CM |
| CA |
此时点A为线段BM的中点．
过点M作MD⊥CA交CA的延长线于点D，则
由
|
∴AD=CA，
∴
| CM |
| CA |
| CD |
| CA |
故答案为18．
点评：本题考查了向量数量积的几何意义，向量加法及数乘的含义，关键是充分利用图形的几何特征，如线段与线段的长度关系，夹角，点的位置变化等，必要时可添加适当的辅助线．
练习册系列答案
相关题目
如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，Q为线段AP的中点，AB=3，BC=4，PA=2，则P到平面BQD的距离为