题目内容
 如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,Q为线段AP的中点,AB=3,BC=4,PA=2,则P到平面BQD的距离为
如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,Q为线段AP的中点,AB=3,BC=4,PA=2,则P到平面BQD的距离为考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:P到平面BQD的距离等于A到平面BQD的距离,利用等体积,即可求点P到平面BQD的距离.
解答:
解:∵Q为线段AP的中点,
∴P到平面BQD的距离等于A到平面BQD的距离,
设A到平面BDQ距离为d,则
∵PA⊥平面ABCD,AQ=1,AB=3,BC=4,
∴BQ=
,DQ=
,BD=5,
∴cos∠BQD=
=
,
∴sin∠BQD=
,
∴S△BQD=
•
•
•
=
,
∵S△BAD=6,
∴由VA-BDQ=VQ-DAB可得
•
•d=
•6•1,
∴d=
.
故答案为:
.
∴P到平面BQD的距离等于A到平面BQD的距离,
设A到平面BDQ距离为d,则
∵PA⊥平面ABCD,AQ=1,AB=3,BC=4,
∴BQ=
| 10 |
| 17 |
∴cos∠BQD=
| 10+17-25 | ||
2
|
| 1 | ||
|
∴sin∠BQD=
| 13 | ||
|
∴S△BQD=
| 1 |
| 2 |
| 10 |
| 17 |
| 13 | ||
|
| 13 |
| 2 |
∵S△BAD=6,
∴由VA-BDQ=VQ-DAB可得
| 1 |
| 3 |
| 13 |
| 2 |
| 1 |
| 3 |
∴d=
| 12 |
| 13 |
故答案为:
| 12 |
| 13 |
点评:本题主要考查了点P到平面BQD的距离的求解,同时考查了推理论证的能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
若5个人站成一排,且要求甲必须站在乙、丙两人之间,则不同的排法有( )
| A、80种 | B、40种 |
| C、36种 | D、20种 |
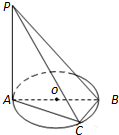 如图,AB是圆O的直径,PA垂直于圆所在的平面,C是圆周上的点.
如图,AB是圆O的直径,PA垂直于圆所在的平面,C是圆周上的点. 如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于
如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于