题目内容
已知正四面体A-BCD中，O为底面正三角形BCD的中心，E为AB中点，求异面直线OE与BC所成角的大小．
考点：异面直线及其所成的角
专题：空间角
分析：取AC的中点F，EF∥BC，∴∠FEO即异面直线OE与BC所成角，再证明△EFO是正三角形，从而求得异面直线OE与BC所成角为60°．
解答：
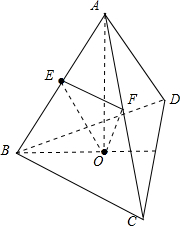解：设AB=a，取AC的中点F，连接EF，连接EO、FO、BO，E为AB中点，∴EF∥BC，∴∠FEO即异面直线OE与BC所成角，
正四面体A-BCD中，O为底面正三角形BCD的中心，∴AO⊥面BCD，BO?面BCD，AO⊥BO，在Rt△ABO中，E为AB中点，
∴OE=
a，同理，OF=
a，又E、F分别为AB、AC中点，∴EF=
a，∴△EFO是正三角形，∴∠FEO=60°
∴异面直线OE与BC所成角为60°
解：设AB=a，取AC的中点F，连接EF，连接EO、FO、BO，E为AB中点，∴EF∥BC，∴∠FEO即异面直线OE与BC所成角，正四面体A-BCD中，O为底面正三角形BCD的中心，∴AO⊥面BCD，BO?面BCD，AO⊥BO，在Rt△ABO中，E为AB中点，
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴异面直线OE与BC所成角为60°
点评：本题考查异面直线所成的角，角的做法是关键．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
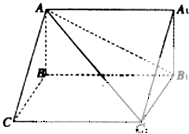如图，在三棱柱ABC-A1B1C1中，已知AB=BC=1，CC1=2，AC1与平面BCC1B1所成角为30°，AB⊥平面BB1C1C．
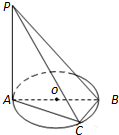如图，AB是圆O的直径，PA垂直于圆所在的平面，C是圆周上的点．
已知直角梯形PBCD，A是PD边上的中点（如图甲），∠D=∠C=