题目内容
以椭圆
+
=1的焦点为顶点,一条渐近线为y=2x的双曲线的方程 .
| x2 |
| 4 |
| y2 |
| 20 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出椭圆
+
=1的焦点坐标,可得双曲线的顶点,根据一条渐近线为y=2x,求出b,从而可求双曲线的方程.
| x2 |
| 4 |
| y2 |
| 20 |
解答:
解:椭圆
+
=1的焦点为(0,±4),
∴双曲线的顶点为(0,±4),
∴a=4,
∵一条渐近线为y=2x,
∴
=2,
∴b=2,
∴双曲线的方程为
-
=1.
故答案为:
-
=1.
| x2 |
| 4 |
| y2 |
| 20 |
∴双曲线的顶点为(0,±4),
∴a=4,
∵一条渐近线为y=2x,
∴
| a |
| b |
∴b=2,
∴双曲线的方程为
| y2 |
| 16 |
| x2 |
| 4 |
故答案为:
| y2 |
| 16 |
| x2 |
| 4 |
点评:本题考查椭圆的性质,考查双曲线的性质与方程,正确求出a,b是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
|
|=1,|
|=2,
=
+
,
⊥
,则
与
的夹角等于( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、90° |
若复数
(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| a-i |
| 1+i |
| A、-1 | B、1 | C、2 | D、-2 |
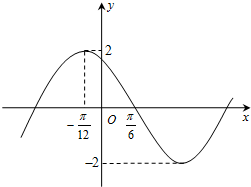 已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )
已知函数f(x)=2sin(wx+φ)(其中x∈R,w>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是( )A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(6x-
| ||
D、f(x)=2sin(6x+
|

