题目内容
在等差数列{an}中,a1=1,a5=9.
(1)求a3;
(2)记bn=2an,证明:数列{bn}是等比数列;
(3)对于(2)中的Sn,求函数f(n)=Sn-t•2n(n∈N*,t为常数且t∈[0,8])的最小值g(t).
(1)求a3;
(2)记bn=2an,证明:数列{bn}是等比数列;
(3)对于(2)中的Sn,求函数f(n)=Sn-t•2n(n∈N*,t为常数且t∈[0,8])的最小值g(t).
考点:数列与函数的综合,等比关系的确定
专题:综合题,等差数列与等比数列
分析:(1)利用等差数列{an}中,a1=1,a5=9,可求a3;
(2)当n≥2时,
=
=2an-an-1=2,可得数列{bn}是等比数列;
(3)f(n)=
(4n-1)-t•2n=
(2n-
)2-
t2-
,即可求函数f(n)=Sn-t•2n(n∈N*,t为常数且t∈[0,8])的最小值g(t).
(2)当n≥2时,
| bn |
| bn-1 |
| 2an |
| 2an-1 |
(3)f(n)=
| 2 |
| 3 |
| 2 |
| 3 |
| 3t |
| 4 |
| 3 |
| 8 |
| 2 |
| 3 |
解答:
解:(1)a3=
=5---------(2分)
(2)由a1=1,a5=9得,an=2n-1
当n≥2时,
=4,
所以数列{bn}是以2为首项,4为公比的等比数列-------(5分)
(3)由(2)可得,Sn=
=
(4n-1)------(7分)
所以,f(n)=
(4n-1)-t•2n=
(2n-
)2-
t2-
∵t∈[0,8],∴
t∈[0,6],而n∈N*
所以,当0≤t≤4时,f(n)min=f(1)=-2t+2
当4<t≤8时,f(n)min=f(2)=-4t+10
故g(t)=
----------(10分)
| a1+a5 |
| 2 |
(2)由a1=1,a5=9得,an=2n-1
当n≥2时,
| bn |
| bn-1 |
所以数列{bn}是以2为首项,4为公比的等比数列-------(5分)
(3)由(2)可得,Sn=
| 2(1-4n) |
| 1-4 |
| 2 |
| 3 |
所以,f(n)=
| 2 |
| 3 |
| 2 |
| 3 |
| 3t |
| 4 |
| 3 |
| 8 |
| 2 |
| 3 |
∵t∈[0,8],∴
| 3 |
| 4 |
所以,当0≤t≤4时,f(n)min=f(1)=-2t+2
当4<t≤8时,f(n)min=f(2)=-4t+10
故g(t)=
|
点评:本题考查等比数列的证明,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
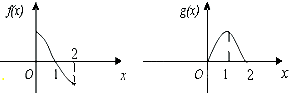 已知偶函数f(x)与奇函数g(x)的定义域都是(-2,2),它们在[0,2]上的图象如图所示,则使关于x的不等式f(x)•g(x)>0成立的x的取值范围为( )
已知偶函数f(x)与奇函数g(x)的定义域都是(-2,2),它们在[0,2]上的图象如图所示,则使关于x的不等式f(x)•g(x)>0成立的x的取值范围为( )| A、(-2,-1)∪(1,2) |
| B、(-1,0)∪(0,1) |
| C、(-2,-1)∪(0,1) |
| D、(-1,0)∪(1,2) |
已知平面向量
,
,
满足|
|=1,|
|=2,|
|=3,且
,
,
两两所成的角相等,则|
+
+
|等于( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
| B、6 | ||
C、6或
| ||
D、6或
|
 已知f(x)是定义域为R的奇函数,当x≥0时,f(x)=x2-2x.
已知f(x)是定义域为R的奇函数,当x≥0时,f(x)=x2-2x.