题目内容
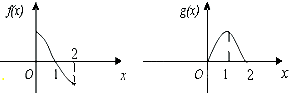已知偶函数f（x）与奇函数g（x）的定义域都是（-2，2），它们在[0，2]上的图象如图所示，则使关于x的不等式f（x）•g（x）＞0成立的x的取值范围为（ ）| A、（-2，-1）∪（1，2） |
| B、（-1，0）∪（0，1） |
| C、（-2，-1）∪（0，1） |
| D、（-1，0）∪（1，2） |
考点：函数奇偶性的性质,函数的图象
专题：函数的性质及应用
分析：观察图象选择函数值同号的部分，再由f（x）是偶函数，g（x）是奇函数，得到f（x）•g（x）是奇函数，从而求得对称区间上的部分，最后两部分取并集．
解答：
解：如图所示：当x＞0时
其解集为：（0，1）
∵y=f（x）是偶函数，y=g（x）是奇函数
∴f（x）g（x）是奇函数
∴当x＜0时，f（x）g（x）＜0
∴其解集为：（-2，-1）
综上：不等式 f（x）•g（x）＞0的解集是 （-2，-1）∪（0，1）
故选：C
其解集为：（0，1）
∵y=f（x）是偶函数，y=g（x）是奇函数
∴f（x）g（x）是奇函数
∴当x＜0时，f（x）g（x）＜0
∴其解集为：（-2，-1）
综上：不等式 f（x）•g（x）＞0的解集是 （-2，-1）∪（0，1）
故选：C
点评：本题主要考查函数的奇偶性在解不等式中的应用，还考查了数形结合，转化，分类讨论等思想方法．
练习册系列答案
名校课堂系列答案
相关题目
给出下列六个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若|
|=|
|，则
=
；
③若
=
，则四边形ABCD是平行四边形；
④平行四边形ABCD中，一定有
=
；
⑤若
=
，
=
，则
=
；
⑥
∥
，
∥
，则
∥
．
其中不正确的命题的个数为（ ）
①两个向量相等，则它们的起点相同，终点相同；
②若|
| a |
| b |
| a |
| b |
③若
| AB |
| DC |
④平行四边形ABCD中，一定有
| AB |
| DC |
⑤若
| m |
| n |
| n |
| k |
| m |
| k |
⑥
| a |
| b |
| b |
| c |
| a |
| c |
其中不正确的命题的个数为（ ）
| A、2个 | B、3个 | C、4个 | D、5个 |
直线x-y-1=0与圆（x-1）2+（y-2）2=4相交于A、B两点，则弦AB的长为（ ）
A、
| ||
B、2
| ||
C、
| ||
D、2
|
下面说法正确的是（ ）
| A、命题“?x∈R，使得x2+x+1≥0”的否定是“?x∈R，使得x2+x+1≥0” |
| B、实数x＞y是x2＞y2成立的充要条件 |
| C、设p，q为简单命题，若“p∨q”为假命题，则“?p∧?q”也为假命题 |
| D、命题“α=0，则cosα=1”的逆否命题为真命题 |
x=
（n＞3），则x是（ ）
| n! |
| 3! |
A、C
| ||
B、C
| ||
C、A
| ||
D、A
|
执行如图所示的程序框图，则输出的复数z是（ ）
A、-
| ||||||
B、-
| ||||||
| C、1 | ||||||
| D、-1 |
已知函数y=f（x）在x=x0处可导，则
等于（ ）
| lim |
| h→0 |
| f(x0)-f(x0-h) |
| h |
| A、f′（x0） |
| B、2f′（x0） |
| C、-2f′（x0） |
| D、0 |
在△ABC中，角A、B、C的对边分别为a、b、c，则acosB+bcosA等于（ ）
A、
| ||
| B、b | ||
| C、c | ||
| D、a |