题目内容
4．若（x+1）n=xn+…+ax3+bx2+…+1（n∈N*），且a：b=3：1，则n的值为11．分析 根据二项式展开式的通项公式，结合题意可得 $\frac{{C}_{n}^{n-3}}{{C}_{n}^{n-2}}$=$\frac{3}{1}$，由此求得a的值．
解答 解：∵（x+1）n=xn+…+ax3+bx2+…+1（n∈N*），且a：b=3：1，
∴$\frac{{C}_{n}^{n-3}}{{C}_{n}^{n-2}}$=$\frac{3}{1}$，即 $\frac{{C}_{n}^{3}}{{C}_{n}^{2}}$=$\frac{\frac{n•（n-1）•（n-2）}{3•2•1}}{\frac{n•（n-1）}{2•1}}$=$\frac{n-2}{3}$，∴n=11，
故答案为：11．
点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．
练习册系列答案
相关题目
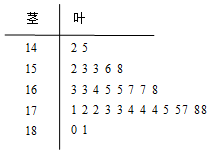从某校的高一学生中采用系统抽样法选出30人测量其身高，数据的茎叶图如图（单位：cm）：若高一年级共有600人，据上图估算身高在1.70m以上的大约有300人．
16．已知锐角三角形三边长分别为1，3，a，则a的取值范围是（ ）
| A． | 8＜a＜10 | B． | 2$\sqrt{2}＜a＜\sqrt{10}$ | C． | $2\sqrt{2}＜a＜10$ | D． | $\sqrt{10}＜a＜8$ |
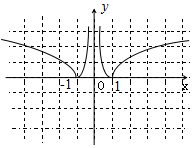已知函数f（x）是定义在{x|x≠0}上的偶函数，且当x＞0时，f（x）=log2x．