Question

19．已知棱长为1，各面均为等边三角形的四面体S-ABC，则它的表面积S=$\sqrt{3}$，体积V=$\frac{\sqrt{2}}{12}$．

Answer 1

分析 由题意画出图形，求出四面体的高，再求出一个等边三角形的面积，乘以4得表面积，代入棱锥体积公式求得体积．

解答 解：如图，四面体S-ABC的各棱长为1，则其四个面均为边长为1的等边三角形，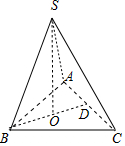
过S作底面垂线，垂足为O，则O为底面三角形的中心，连接BO并延长，交AC于D．
则BD=$\sqrt{1-（\frac{1}{2}）^{2}}=\frac{\sqrt{3}}{2}$，BO=$\frac{2}{3}BD=\frac{2}{3}×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$．
∴SO=$\sqrt{1-（\frac{\sqrt{3}}{3}）^{2}}=\frac{\sqrt{6}}{3}$．
∴正四面体的表面积S=4×$\frac{1}{2}×1×\frac{\sqrt{3}}{2}=\sqrt{3}$；
体积V=$\frac{1}{3}×\frac{1}{2}×1×\frac{\sqrt{3}}{2}×\frac{\sqrt{6}}{3}=\frac{\sqrt{2}}{12}$．
故答案为：$\sqrt{3}$，$\frac{{\sqrt{2}}}{12}$．

点评 本题考查棱柱、棱锥、棱台的体积的求法，考查空间想象能力和思维能力，是中档题．