题目内容
15.已知数列{an}的前n项和为Sn,且满足${a_1}=\frac{1}{2},{a_n}+2{S_n}{S_{n-1}}=0(n≥2)$.①数列$\left\{{\frac{1}{S_n}}\right\}$是否为等差数列?并证明你的结论;
②求Sn;
③求证:$S_1^2+S_2^2+S_3^2+…+S_n^2<\frac{1}{2}$.
分析 ①由${a_1}=\frac{1}{2},{a_n}+2{S_n}{S_{n-1}}=0(n≥2)$.可得Sn-Sn-1+2SnSn-1=0,化为:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,即可证明.
②利用等差数列的通项公式即可得出.
③n≥2时,${S}_{n}^{2}$=$\frac{1}{4{n}^{2}}$<$\frac{1}{4}\frac{1}{n(n-1)}$=$\frac{1}{4}(\frac{1}{n-1}-\frac{1}{n})$.利用“裂项求和”与数列的单调性即可得出.
解答 ①解:∵${a_1}=\frac{1}{2},{a_n}+2{S_n}{S_{n-1}}=0(n≥2)$.
∴Sn-Sn-1+2SnSn-1=0,化为:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,
∴数列$\left\{{\frac{1}{S_n}}\right\}$为等差数列,公差为2,首项为2.
②解:$\frac{1}{{S}_{n}}$=2+2(n-1)=2n.
∴Sn=$\frac{1}{2n}$.
③证明:n≥2时,${S}_{n}^{2}$=$\frac{1}{4{n}^{2}}$<$\frac{1}{4}\frac{1}{n(n-1)}$=$\frac{1}{4}(\frac{1}{n-1}-\frac{1}{n})$.
∴${S}_{1}^{2}+{S}_{2}^{2}$+…+${S}_{n}^{2}$≤$\frac{1}{4}$+$\frac{1}{4}$$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})]$=$\frac{1}{2}-\frac{1}{n}$<$\frac{1}{2}$.
点评 本题考查了等差数列的定义通项公式、“裂项求和”与数列的单调性、数列递推关系,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案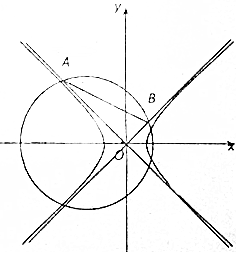 如图,双曲线k2x2-y2=1(k>0)的两条渐近线与圆(x+2)2+y2=5在x轴的上方交于A、B两点.
如图,双曲线k2x2-y2=1(k>0)的两条渐近线与圆(x+2)2+y2=5在x轴的上方交于A、B两点.